逻辑回归代价函数

blacklad大约 3 分钟AIAI

1 不使用平方误差函数

对于逻辑回归，如果使用平方误差函数：

J \left( \vec{w}, b \right) = \frac{1}{m}\sum\limits_{i=1}^m \frac{1}{2}\ \left( f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)} \right)^{2}

得到的代价函数会变成一个非凸的函数，会存在很多局部的极小值，任意一个局部极小值都可能让梯度下降法收敛，所以平方误差函数不适合作为逻辑回归的代价函数。

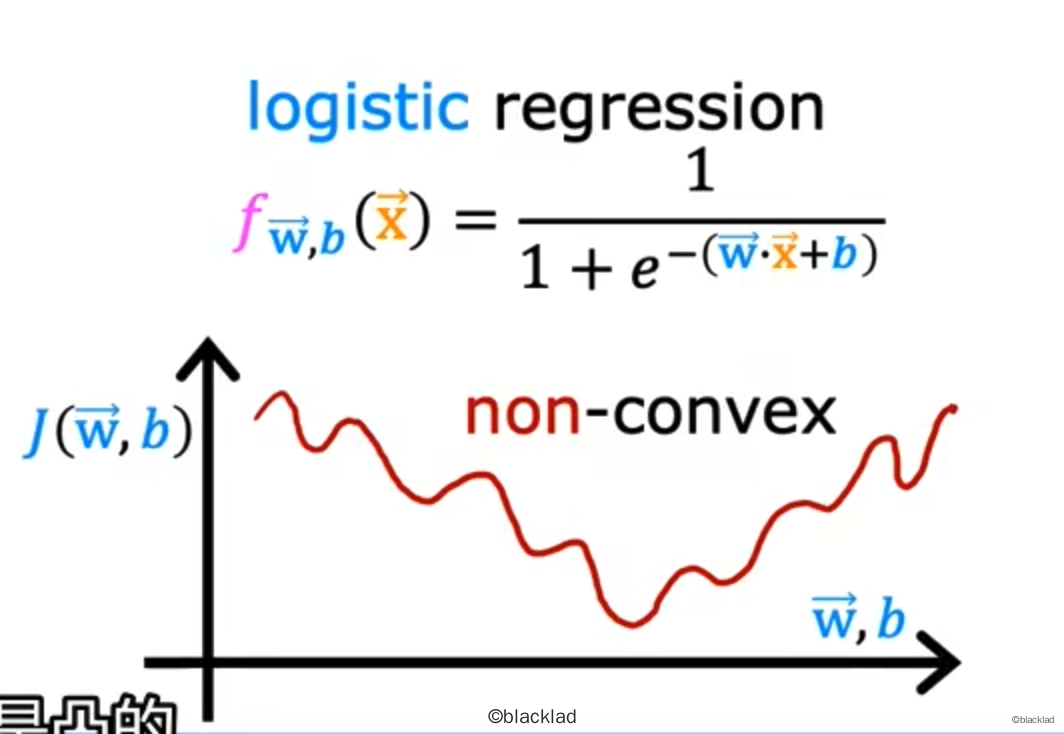
一般使用损失函数来作为逻辑回归的成本函数的一部分。损失函数表示单个训练样本的损失。

L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})=\begin{cases}\quad-log(f_{\vec{w},b}(\vec{x}^{(i)})), y^{(i)}=1,\\-log(1-f_{\vec{w},b}(\vec{x}^{(i)})), y^{(i)}=0.&\end{cases}

当 $y^{(i)}=1$ 时，且 $0 <= f_{\vec{w},b}(\vec{x}^{(i)}) <= 1$ ， $-log(f_{\vec{w},b}(\vec{x}^{(i)}))$ 的函数如图所示：

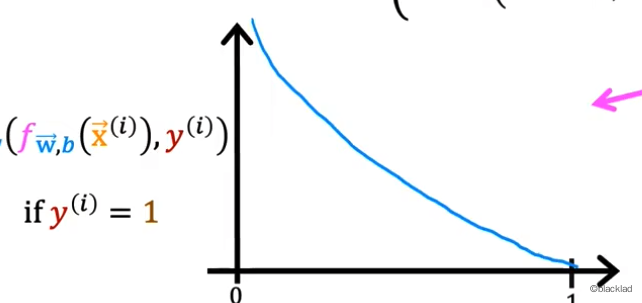
可以看到当预测值 $f_{\vec{w},b}(\vec{x}^{(i)})$ 越接近实际值 $y^{(i)}=1$ 时，损失函数的值L就越小。

当 $y^{(i)}=0$ 时，且 $0 <= f_{\vec{w},b}(\vec{x}^{(i)}) <= 1$ ， $-log(1 - f_{\vec{w},b}(\vec{x}^{(i)}))$ 的函数如图所示：

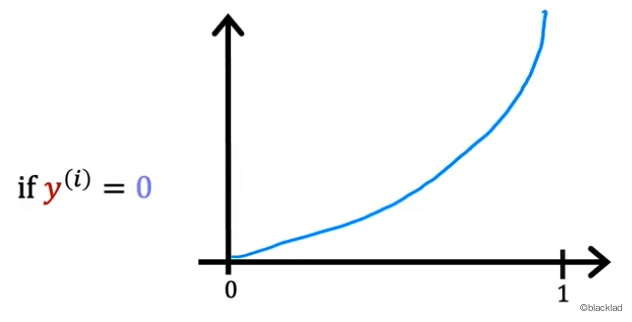
可以看到当预测值 $f_{\vec{w},b}(\vec{x}^{(i)})$ 越接近实际值 $y^{(i)} = 0$ 时，损失函数的值就越小。

所以损失函数L对于任意一种情况，当预测值越接近真实值，损失值就越小，越远离真实值，损失值就越大，符合代价函数的定义。

对所有样本的损失值求和得到的代价函数为:

J(\vec{w},b)=\frac1m\sum_{i=1}^mL(f_{\vec{w},b}\left(\vec{x}^{(i)}\right),y^{(i)})

由于分类问题是二元分类问题， $y^{(i)}$ 只有0/1两种取值，所以可以对损失函数的公式可以进行简化如下：

L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})=-y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))-(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))

简化后的代价函数如下：

J(\vec{w},b)=-\frac1m\sum_{i=1}^m[y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))]

参考最大似然估计(maximum likehood estimation)

为了获得代价函数 $J(\vec{w},b)$ 的最小值，依然可以使用梯度下降法。

先求偏导数:

\frac{\partial J(\vec{w}, b)}{\partial w_j} = \frac{1}{m} \sum_{i=1}^{m} \left[ f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)} \right] x_j^{(i)}

\frac{\partial J(\vec{w}, b)}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} \left[ f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}\right]

即可通过梯度下降不断更新 w 和 b:

w_{j}=w_{j}-\alpha\left[\frac{1}{m}\sum_{i=1}^{m} (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x_{j}^{(i)}\right]

b=b-\alpha\left[\frac{1}{m}\sum_{i=1}^{m} (f_{\vec{w},b}\big(\vec{x}^{(i)}\big)-y^{(i)}) \right]