多维特征

1 介绍

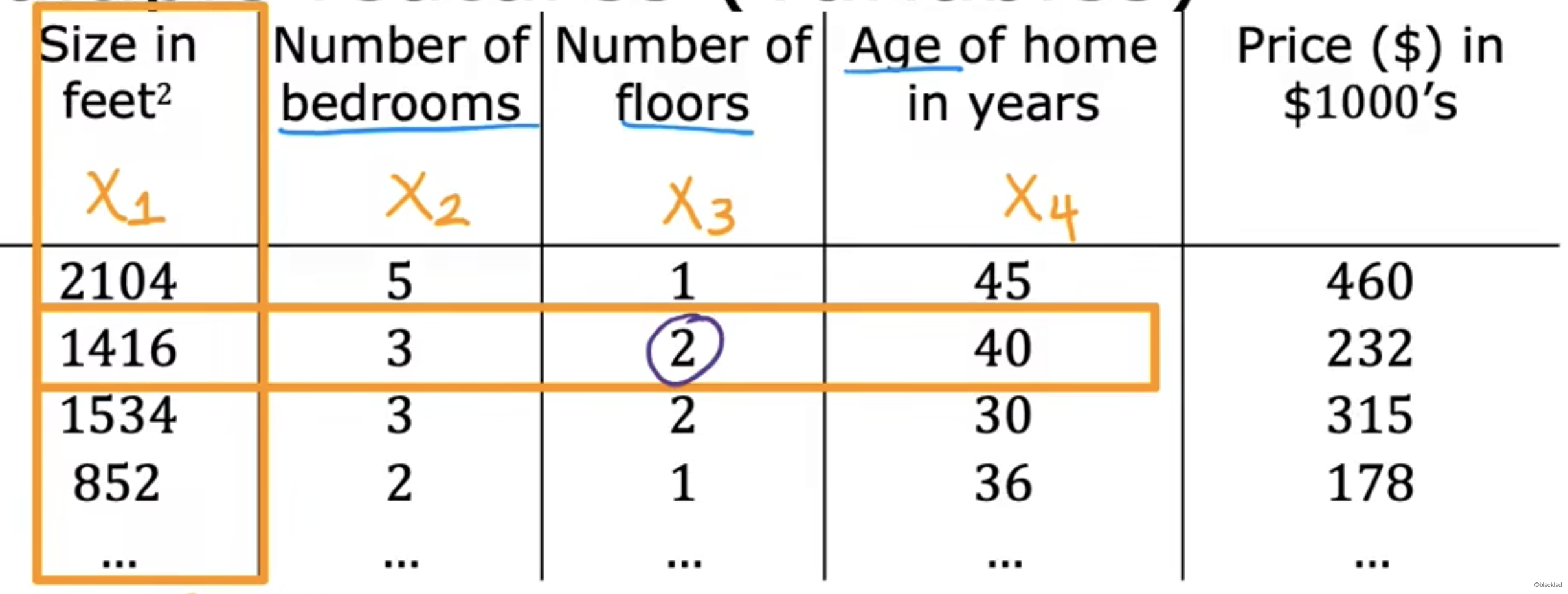
多维特征（multiple linear regression）指多个特征的线性回归模型，如房子的价格由大小、卧室个数、几层和年龄这些共同决定的。

• $x_j$：第 j 列特征
• n：特征的个数
• $\vec{x}^{(i)}$：第 i 行训练数据中的所有的特征
• $x_j^{(i)}$：第 i 行的训练示例的第j列特征

2 模型

使用向量表示模型

$$f_{w,b}(x) = w_1x_1 + w_2x_2 + ... + w_nx_n + b$$

令 $\vec{w} = [w_1, w_2, ... , w_n]$，b是一个数字，$\vec{x} = [x_1, x_2, ... , x_n]$

模型可以用两个向量的点积来表示。

$$f_{\vec{w},b}(\vec{x}) = \vec{w} \cdot \vec{x} + b$$

3 梯度下降

代价函数变为

$$J \left( \vec{w}, b \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)} \right)^{2}$$

梯度下降：

$$w_j = w_j - α\frac{1}{m} \sum\limits_{i=1}^m(f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})x_j^{(i)}$$

$$b = b - \frac{1}{m} \sum\limits_{i=1}^m(f_{w,b}(x^{(i)}) - y^{(i)})$$