逻辑回归

1 分类问题

对于分类问题，它的输出是有限个值。

如果只有两种可能的分类，被称为二元分类，如是否为垃圾邮件，是否为恶性肿瘤等。一般使用yes/no true/false 0/1 来表示。

1.1 肿瘤分类

如下示意图中，1表示恶性的肿瘤，0表示良性的。

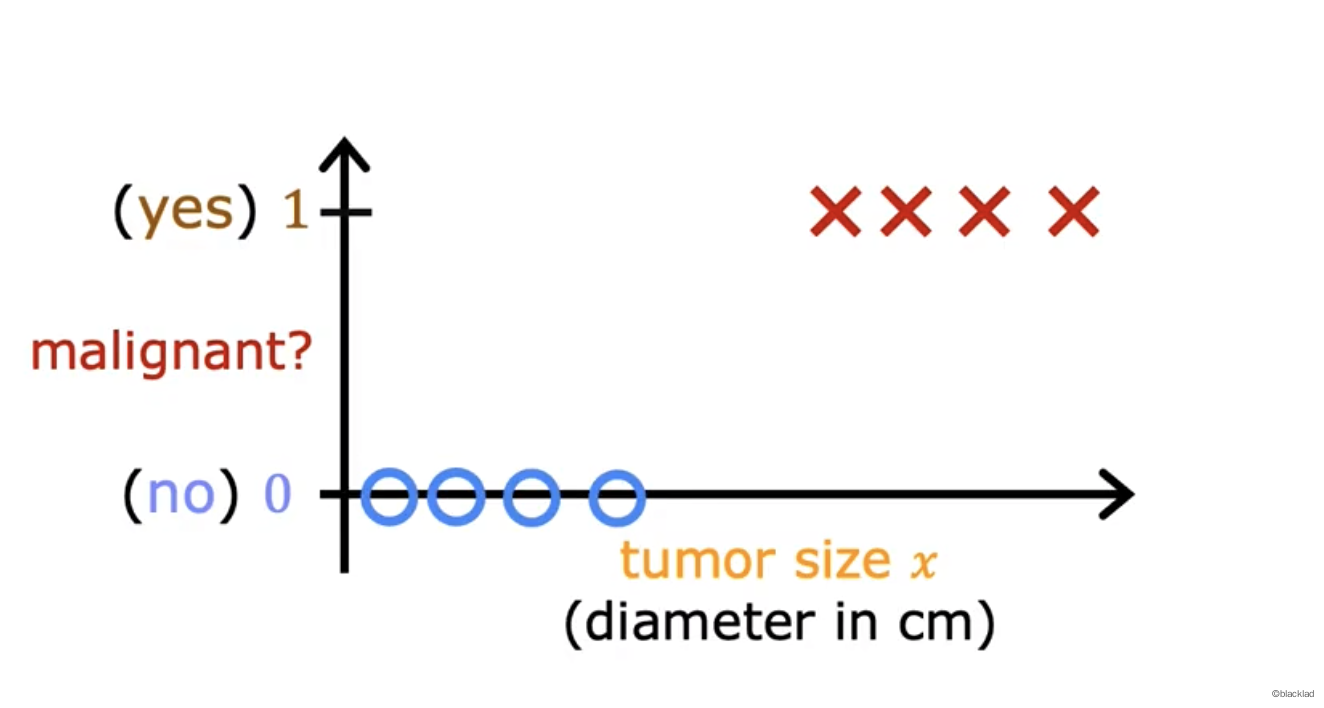
当使用线性回归时，拟合出如下图的直线。可以指定一个阈值，比如 y的值如果大于 0.5 ，表示是恶性肿瘤。

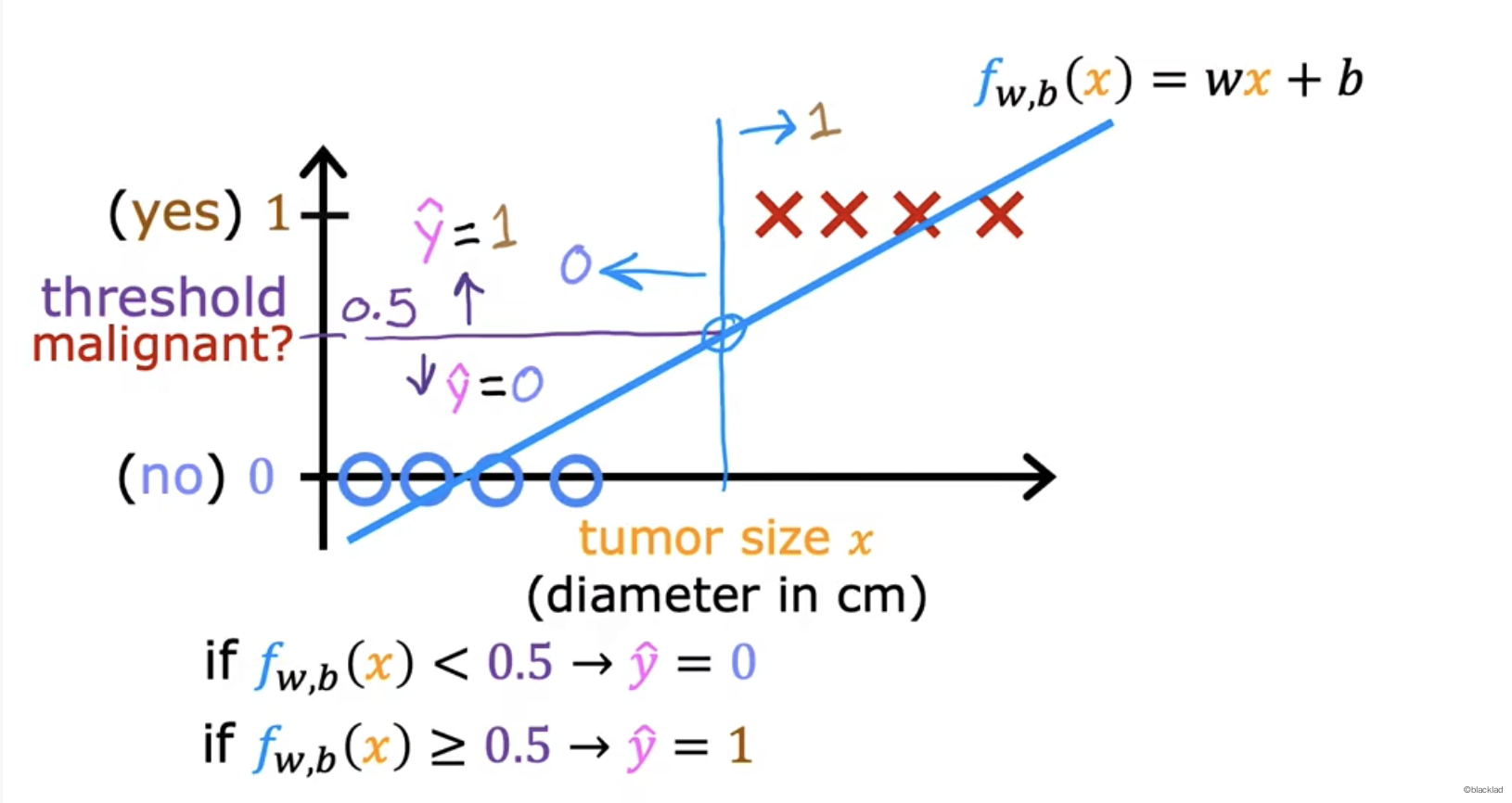
但是当数据不均匀时，比如下图，在右侧再添加一个数据，假设阈值还是0.5，就会把原来判断为是肿瘤的区域变成良性区域，误差就会变大。

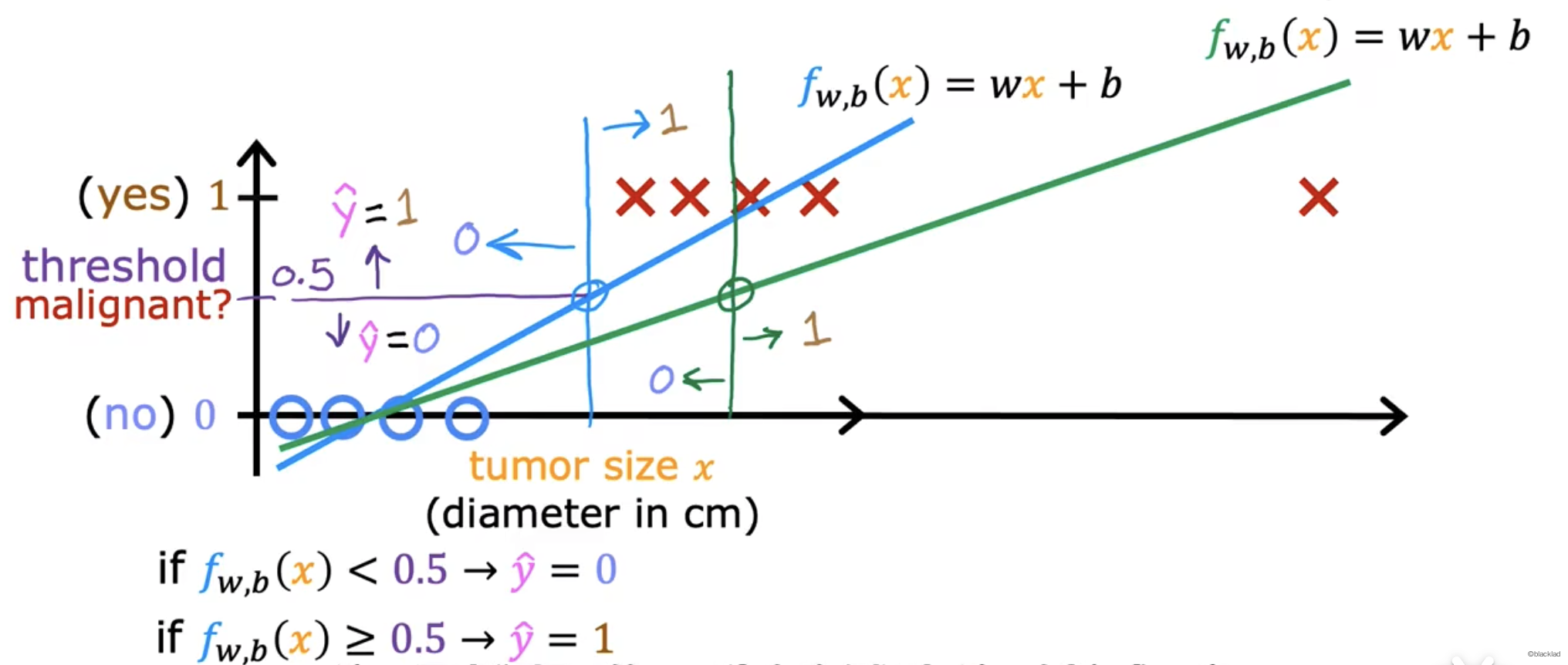
2 逻辑回归

logistic regression，虽然名称中有回归，但实际上是用来解决分类问题。

逻辑回归使用 S 型曲线来进行函数拟合。

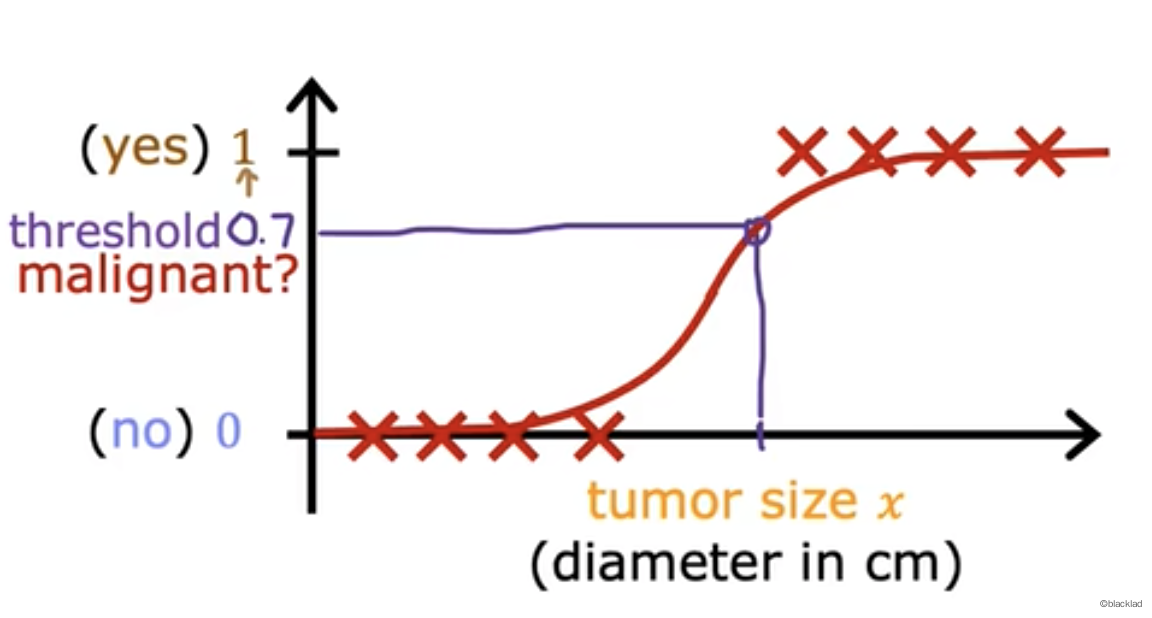
2.1 Sigmoid function

Sigmoid function是一种常见的S型曲线，也被称作逻辑函数。

$$g(z) = \frac{1}{1+e^{-z}}$$

1. $0< g(z) <1$
2. $g(0) = 0.5$
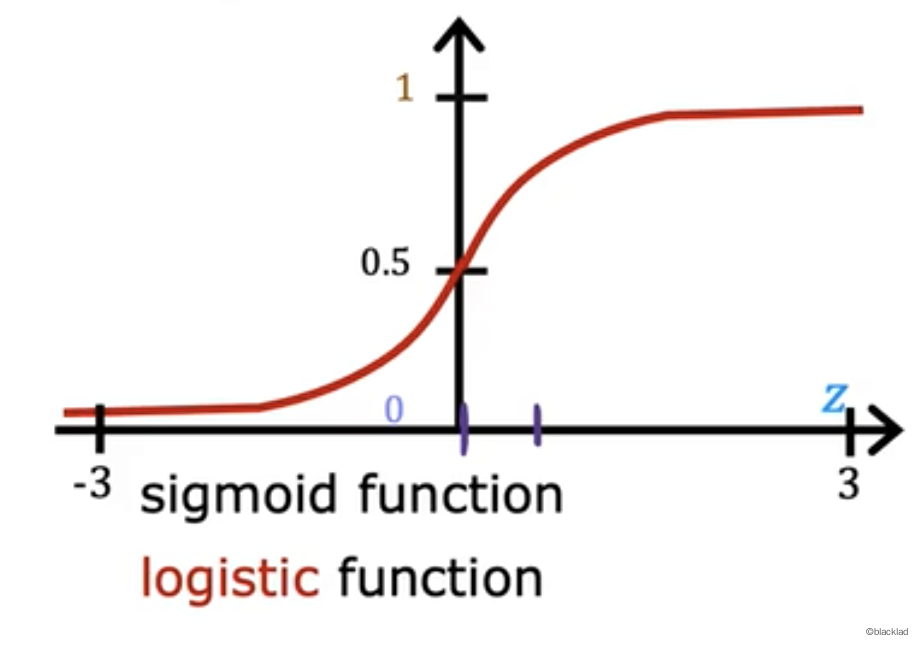
3. z 越大，$e^{-z}$ 接近0，g(z) 越接近1
4. z 越小，$e^{-z}$ 接近无穷大，g(z) 越接近0

这里可以令 $z = \vec{w}\vec{x} + b$，将 z 带入 Sigmoid 函数中既可以得到逻辑回归模型。

$$f_{\vec{w},b}(\vec{x}) = g(z) = g(\vec{w}\vec{x} + b) = \frac{1}{1+e^{-(\vec{w}\vec{x} + b)}}$$

它可以输入一组特征数据，输出一个介于0和1之间的数字。因为函数是连续的，所以最终的结果可以看做 y 取1的概率。

比如得到 $f_{\vec{w},b}(\vec{x}) = 0.7$，那么表示有 70% 的概率是恶性肿瘤，30%的概率为良性的肿瘤。且 P(y = 0) + P(y = 1) = 1。