线性回归模型

1 标准术语

• Training set: 训练数据集，已知的数据。
• x：输出变量，特征值
• y：输出变量，目标变量
• m：训练数据集的总数
• (x, y) ：单个训练样本
• ($X^i$, $Y^i$) ：第i个训练样本

2 流程

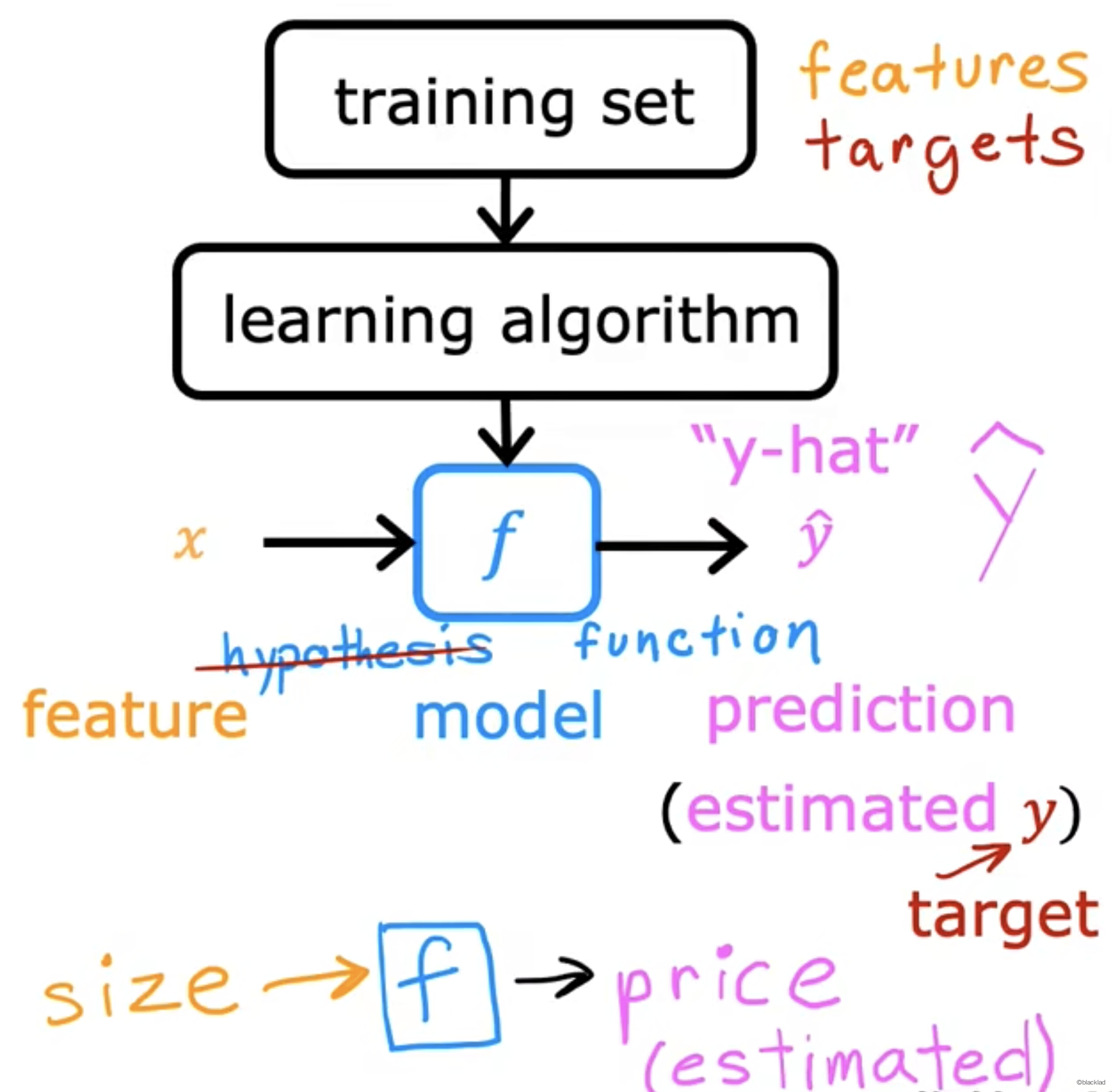
先通过训练集里的房屋价格，给到学习算法，输出一个函数用 f 来表示，对于函数 f 输入是房屋的面积，输出是对价格的估计。

$\hat{y}$是对y的估计或者预测。

f 称作为 model。

3 模型

这里的模型 f 用线性函数来表示。

$f_{w,b}(x) = wx + b$ 或者 $f(x) = wx + b$

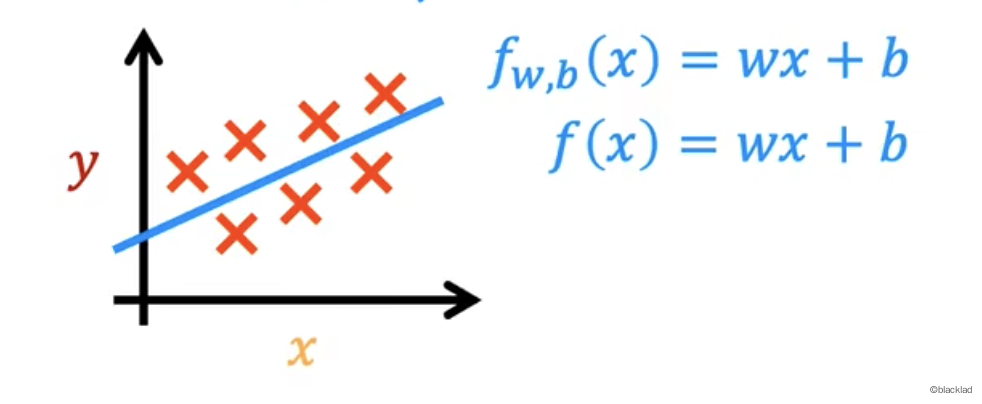
也可以使用非线性函数，如双曲线、抛物线等更复杂的曲线来拟合数据。

4 代价函数 cost function

如何才能得到最符合数据的 $f(x)$。

对于线性函数$f_{w,b}(x) = wx + b$ ，对于不同的参数 w 和 b，会得到不同的直线。

4.1 误差

对于一个输入变量 $x^{(i)}$, $\hat{y}^{(i)}$为预测的值，$y^{(i)}$为输出变量

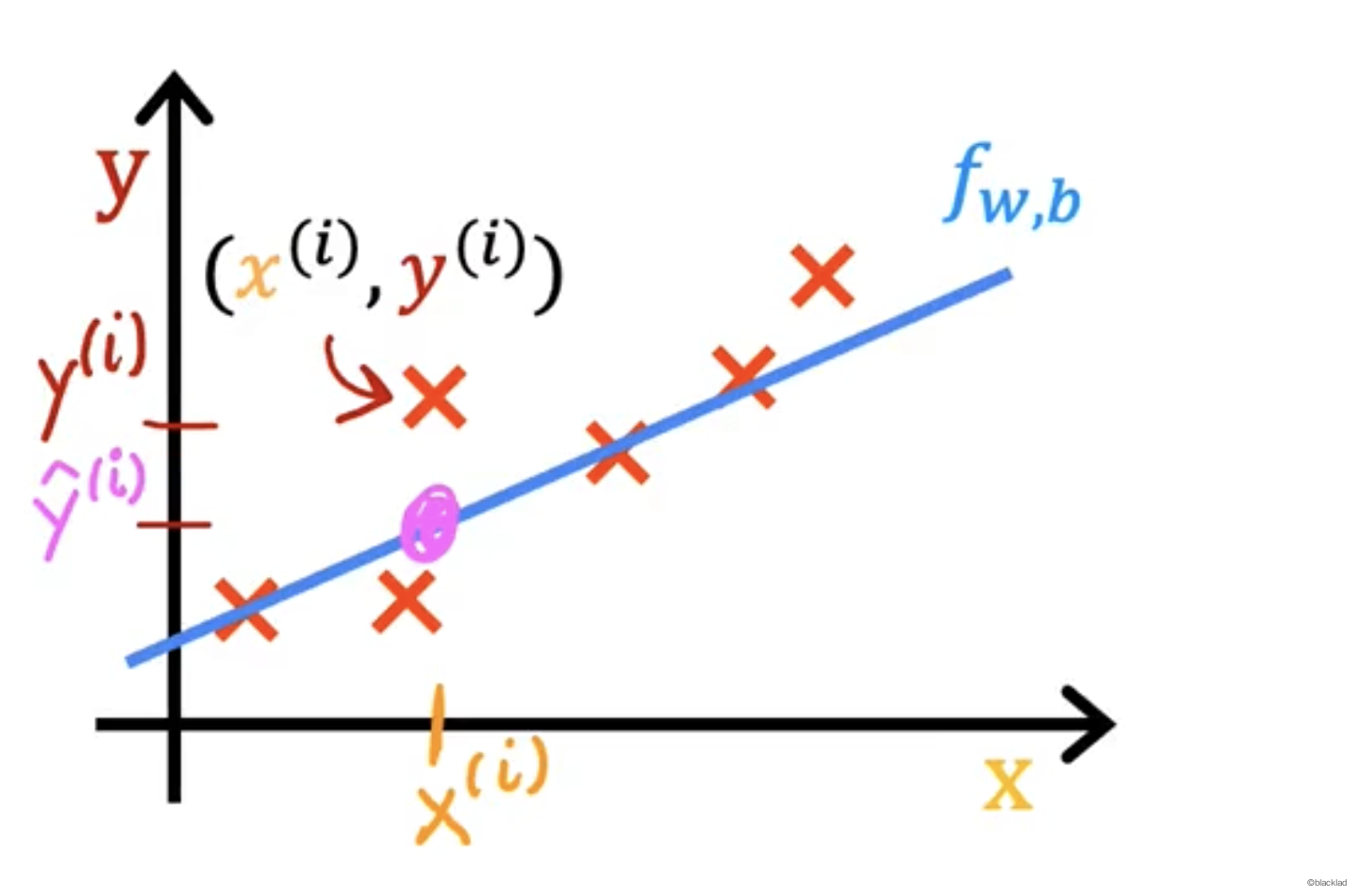
对于所有的训练数据集，找到 w, b 使得$\hat{y}^{(i)}$最接近真实的目标 $y^{(i)}$。

1. 定义误差值 error = $\hat{y}^{(i)}$ - $y^{(i)}$。

2. 为了忽略 负数，取误差的平方并对所有的数据求和 $\sum\limits_{i=1}^m \left( \hat{y}^{(i)}-y^{(i)} \right)^{2}$。

3. 取平均值（要不然数据集越大，误差越大）， $\frac{1}{m} \sum\limits_{i=1}^m \left( \hat{y}^{(i)}-y^{(i)} \right)^{2}$。

4. 再除以2（为了后续计算方便，并不影响最小值），$\frac{1}{2m}\sum\limits_{i=1}^m \left( \hat{y}^{(i)}-y^{(i)} \right)^{2}$。

5. 再将 $\hat{y} = f_{w,b}(x)$这样就得到了代价函数。

$J \left( w, b \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( f_{w,b}(x^{(i)})-y^{(i)} \right)^{2}$

代价函数衡量预测结果与实际结果之间的差异，找到代价函数的取值最小时的 w 和 b。

4.2 例子

一个参数w

为了更好的观察，先假设参数b的值为0。

用一个 $f_w(x) = wx$ 的函数作为模型，简化后的代价函数变为：

$$J \left( w \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( f_{w}(x^{(i)})-y^{(i)} \right)^{2} => J \left( w \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( wx^{(i)}-y^{(i)} \right)^{2}$$

现在模型只有一个参数 w。

训练数据

x	y
1	1
2	2
3	3

x->y 的函数如下图。

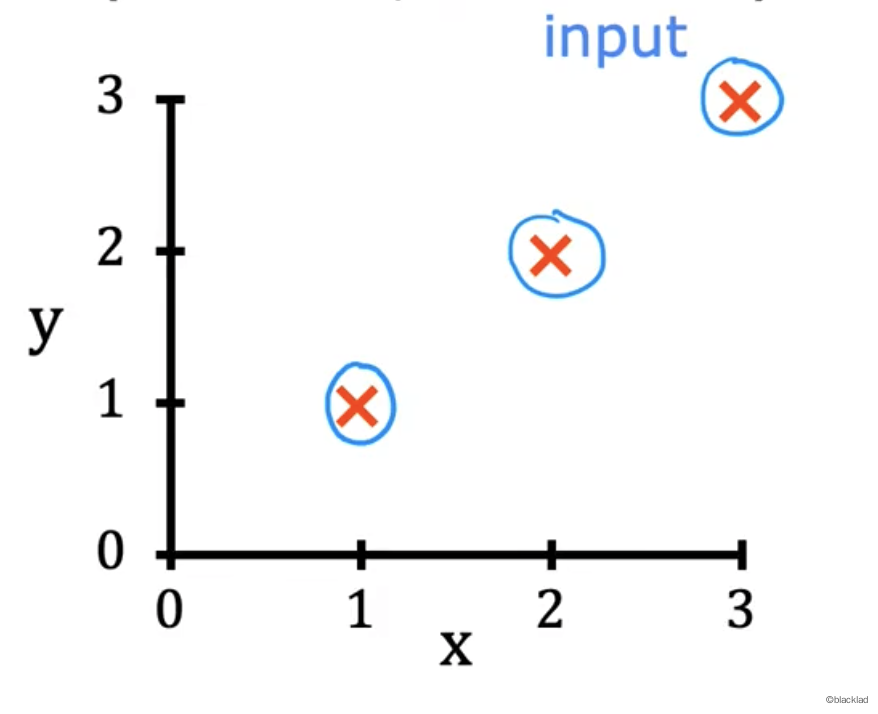
1. 当w = 1时：

x	y	$\hat{y}$	Error $\hat{y} - y$
1	1	1	0
2	2	2	0
3	3	3	0

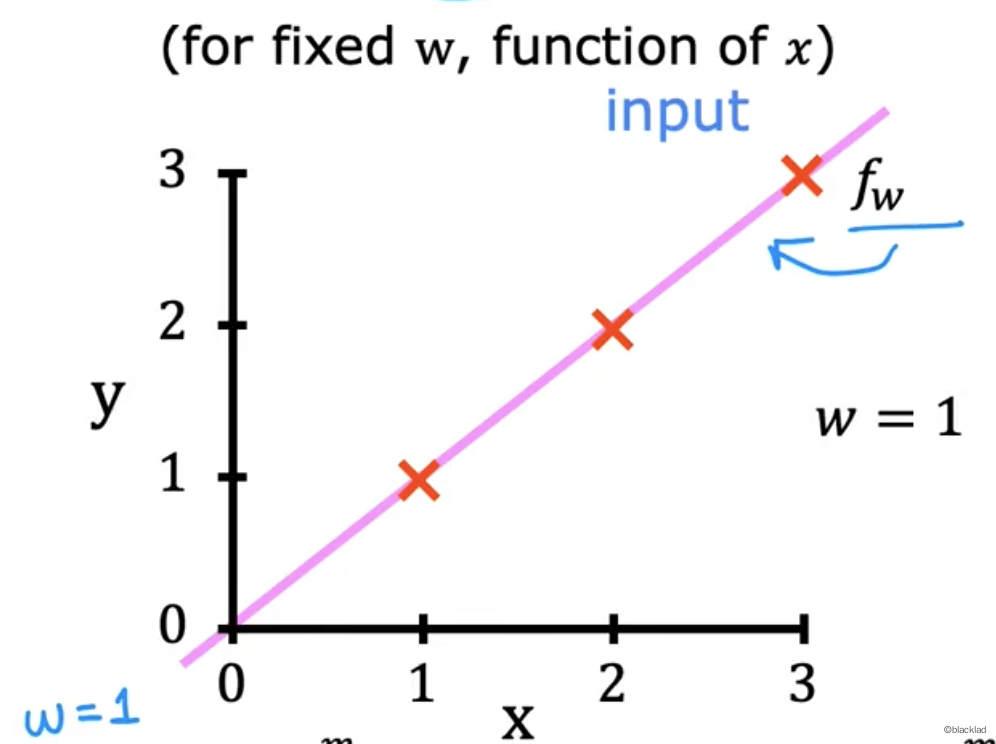
得到当 w = 1 时，带入代价函数公式得到

$$J = \frac{1}{2*3} (0^2 + 0^2 + 0^2) = 0$$

2. 当 w = 0.5 时：

x	y	$\hat{y}$	Error $\hat{y} - y$
1	1	0.5	-0.5
2	2	1	-1
3	3	1.5	-1.5

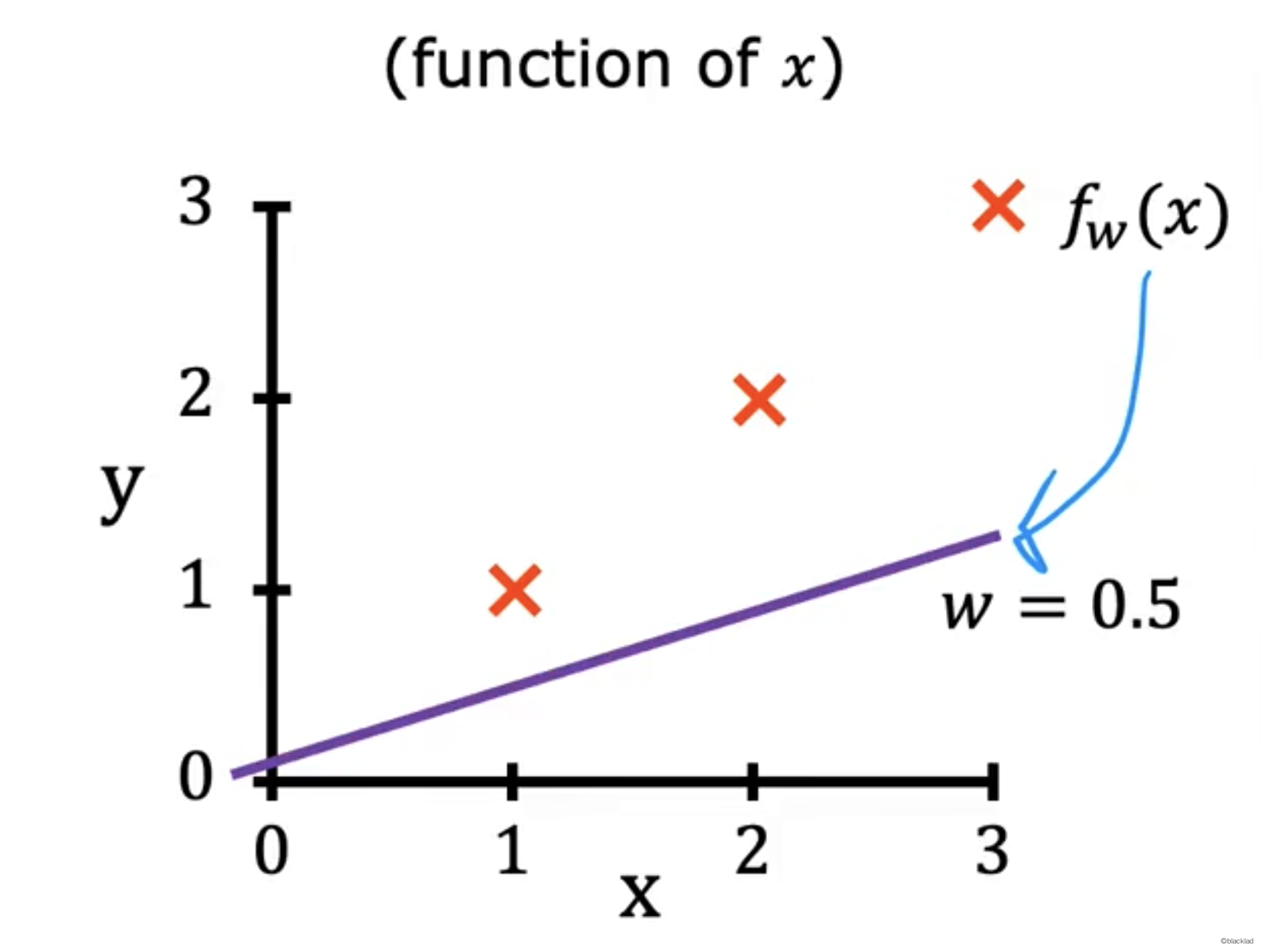
得到当 w = 0.5 时，带入代价函数公式得到

$$J = \frac{1}{2*3} ((-0.5)^2 + (-1)^2 + (-1.5)^2) = 0.58$$

在J(w)的函数图像中找到对应的点。

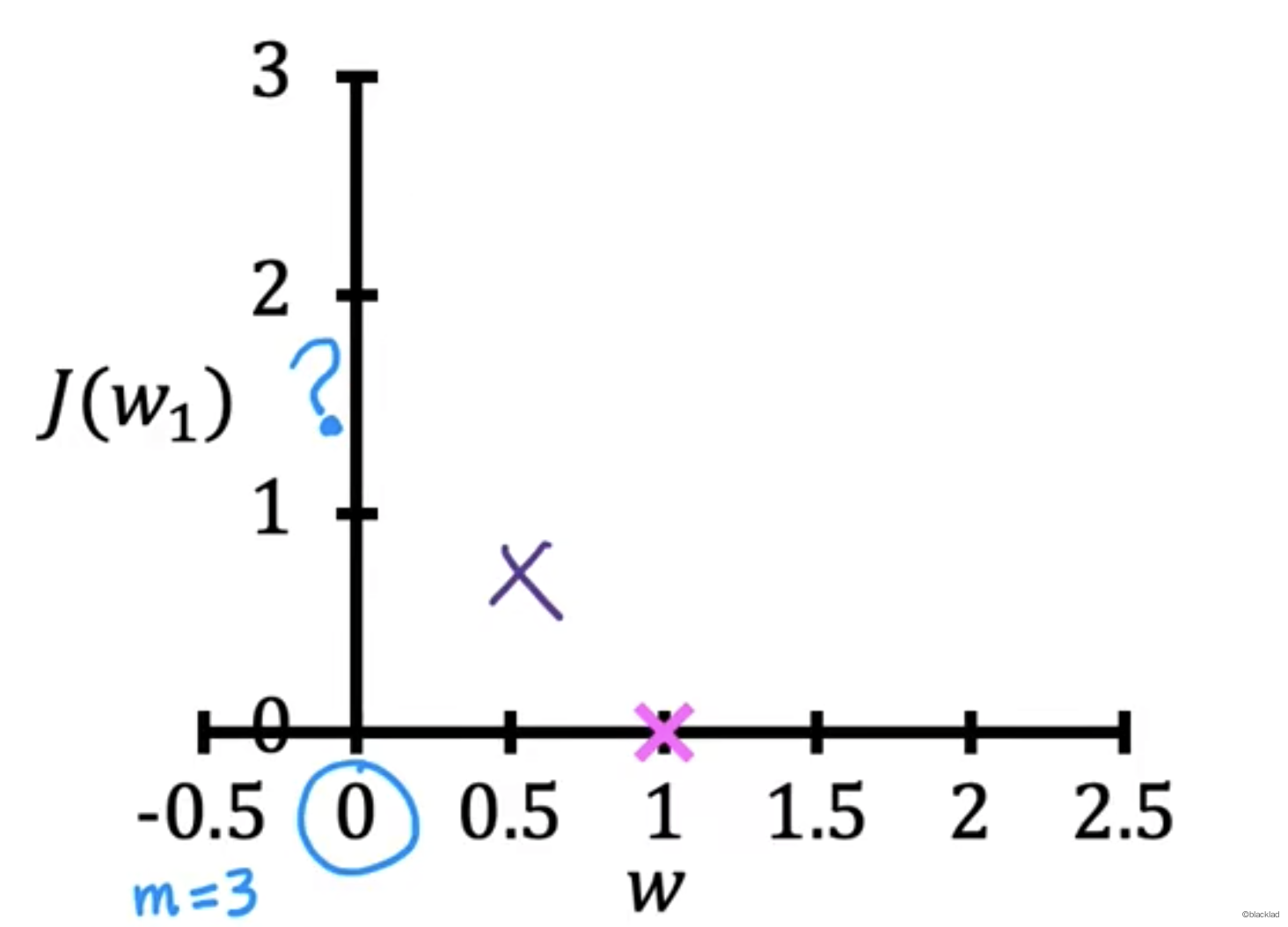
用更多的 w 可以得到一条 J(w)的函数图像。

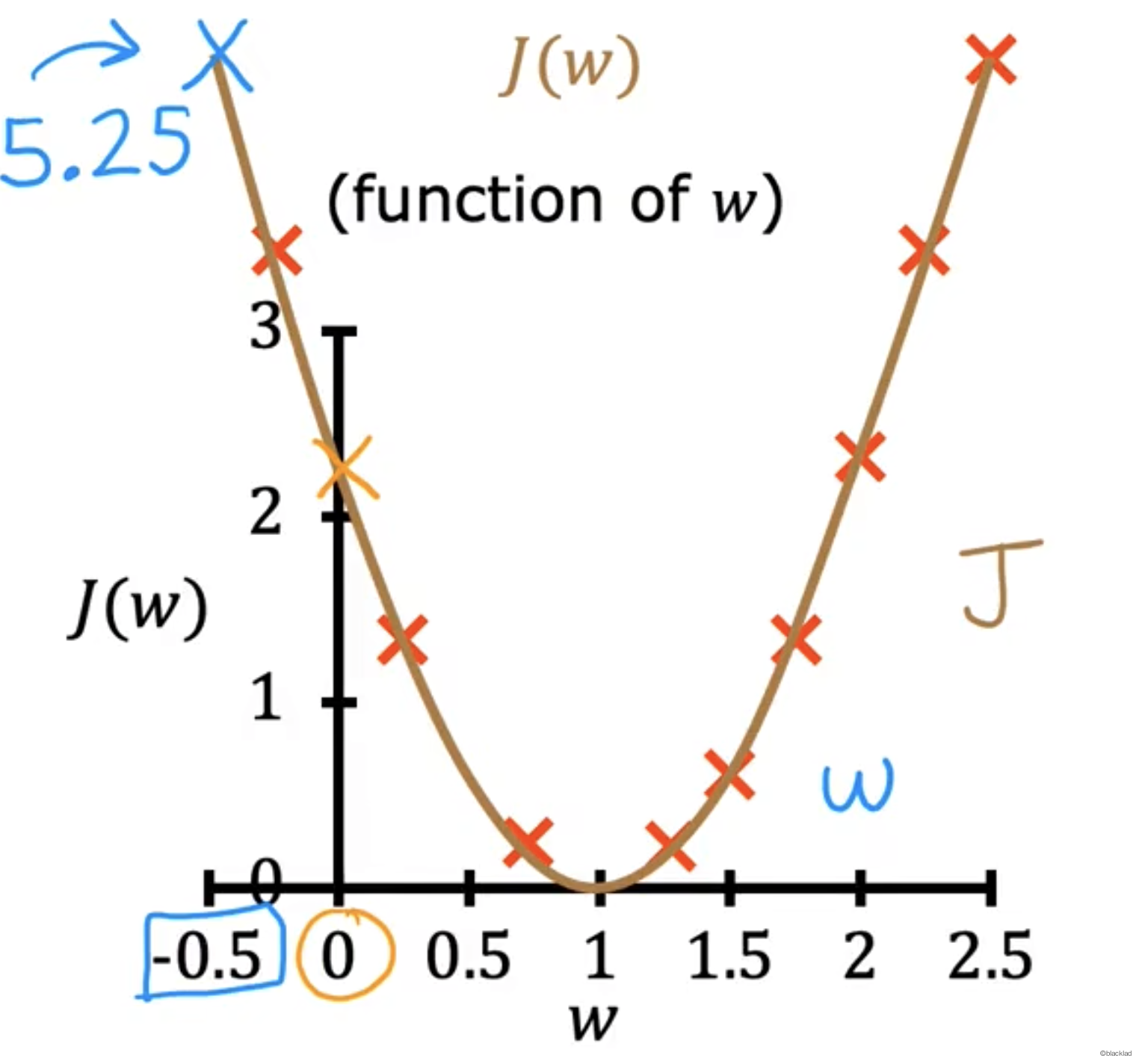
可以看出当 w = 1 时，J(w) 的结果最小。此时 $f_w(x)$ 函数的拟合程度最好。

w b 两个参数

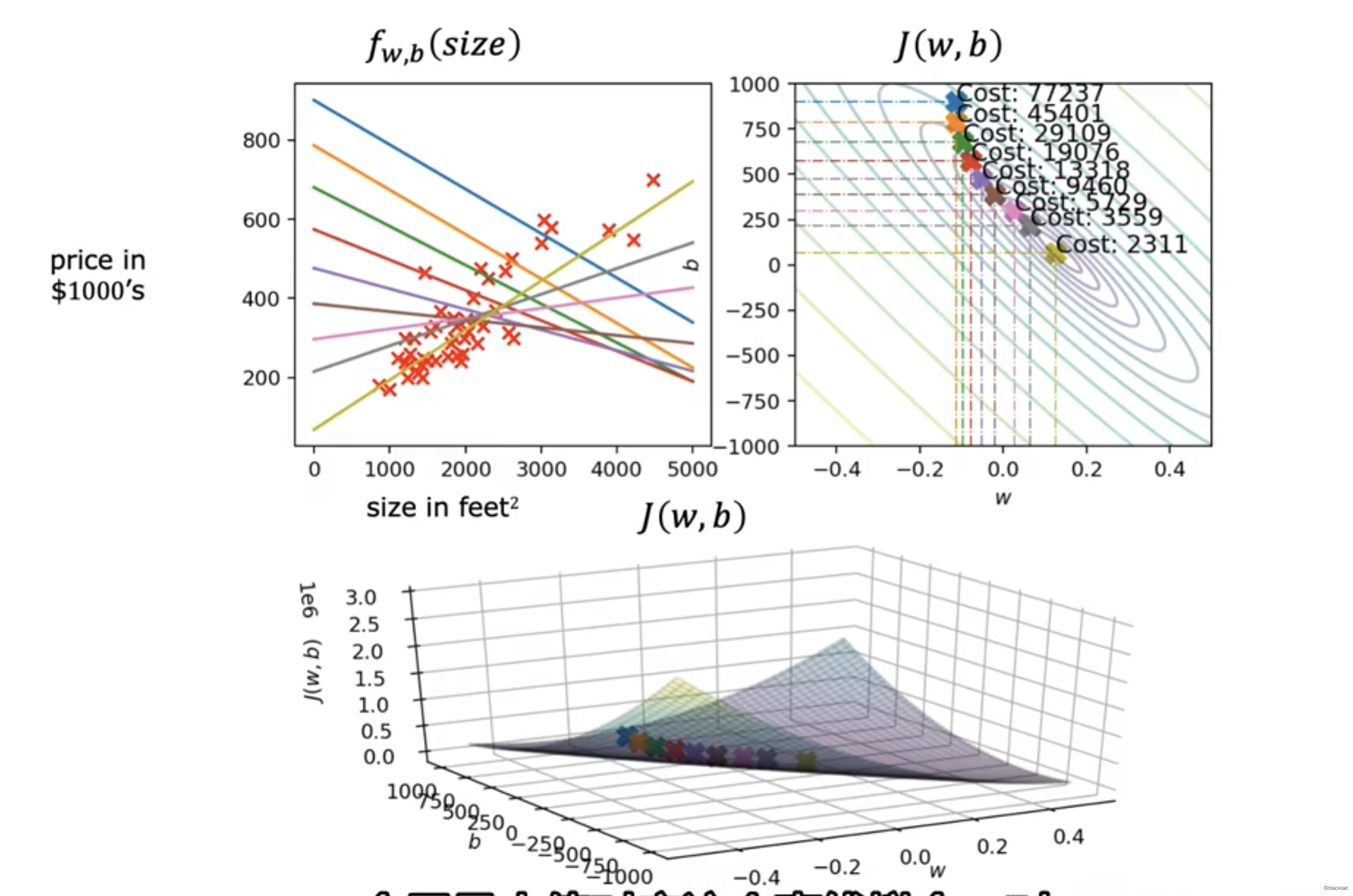
同时将w、b两个参数考虑进去后，得到的代价函数就变成了一个三维的函数图像，类似于一个碗的形状。

对于不同的 w，b 在图像上可以得到一个函数 J 的值。

也可以在 w,b 的平面上用等高线来分析。每条线对应的代价函数的值是一样的。越接近中心代价函数的值越小。

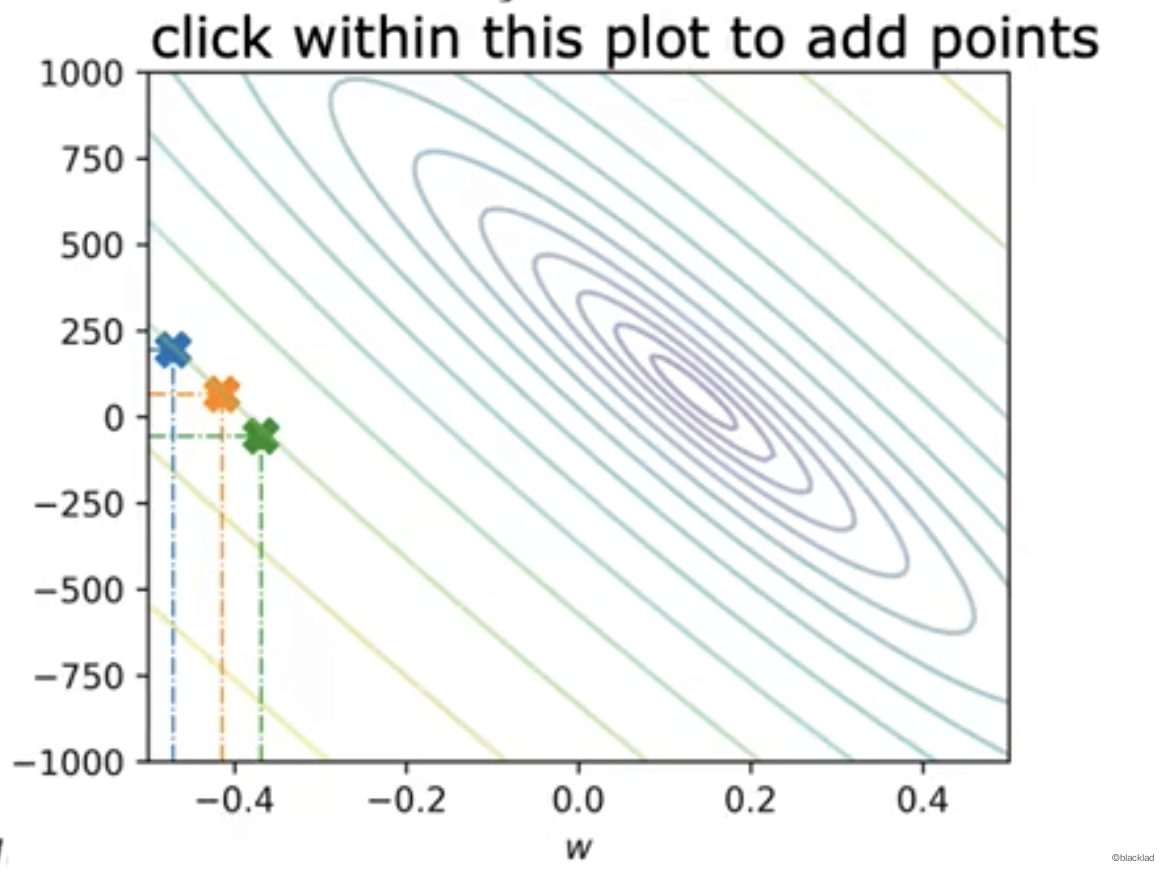
每个点对应的函数如下图。

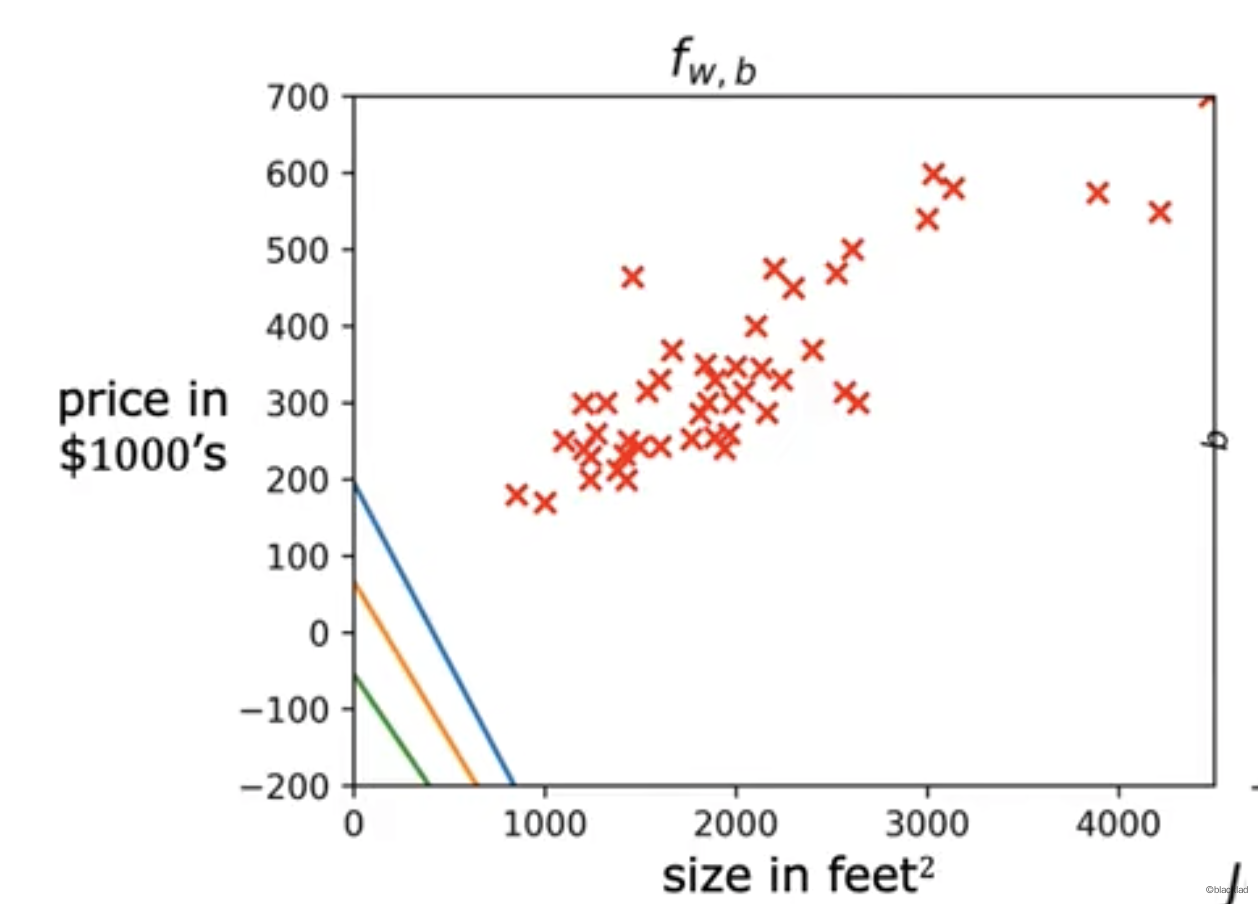
5 梯度下降

由于代价函数是一个复杂的多元函数，很难直接求解得到其最小值。

通过梯度下降 (Gradient Desent) 可以寻找某函数的最小值。

5.1 流程

1. 选择初始点，在函数的取值范围内，选择起始点，一般可以设置 w=0,b=0 作为起始的值。

2. 改变 w,b 不断的调整 w和b，让代价函数的值 J (w,b) 不断的减小

3. 直到找到 J 的最小值，或者最小值的附近

5.2 梯度下降算法

$$w = w - α\frac{∂}{∂w}J(w,b)$$

$$b = b - α\frac{∂}{∂b}J(w,b)$$

1. α 是学习率的意思，控制梯度下降的步幅。是0-1之间的一个很小的正数。
2. $\frac{∂}{∂w}J(w,b)$ 是 J(w,b) 对 w 的偏导数。
3. $\frac{∂}{∂w}J(w,b)$ 是 J(w,b) 对 b 的偏导数。

需要注意这里的 w，b需要同时更新，不能用第一步得到的w，去算第二步的b。

这里减去导数，是因为沿着导数的反方向改变参数（导数结果为正，说明函数在这里递增，参数需要减小。反之导数结果为负，说明函数在这里递减，参数值要增大）

5.3 例子

假设只有一个参数w，求函数 J(w) 的最小值。

$$w = w - α\frac{∂}{∂w}J(w)$$

假设在函数上选取一点

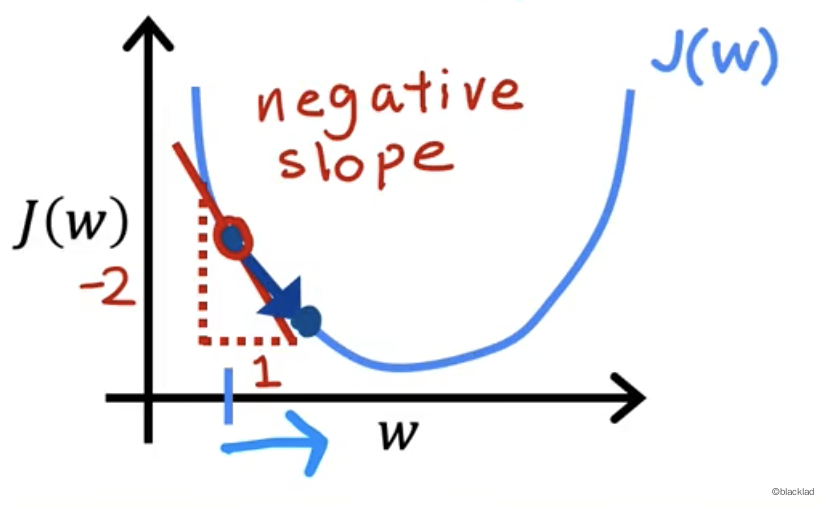
易知这点的导数大于 0 ，α 也大于0，所以 w 的值变小。

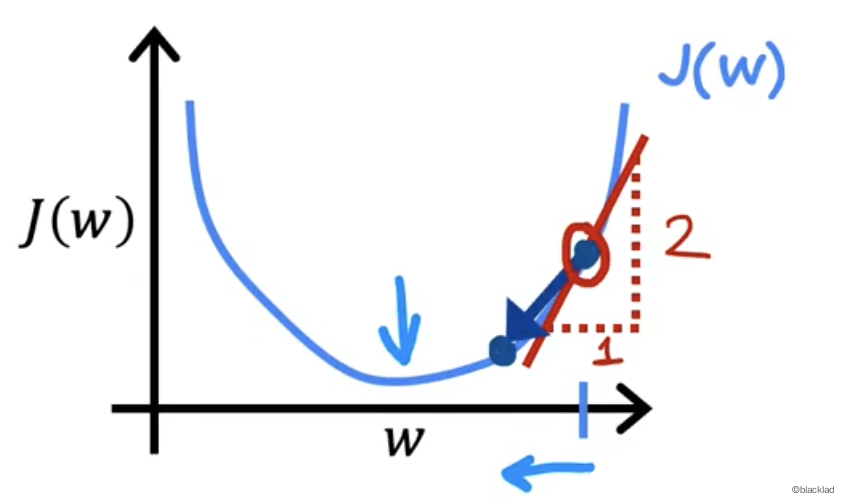
假设这一点选取在了函数的左侧。

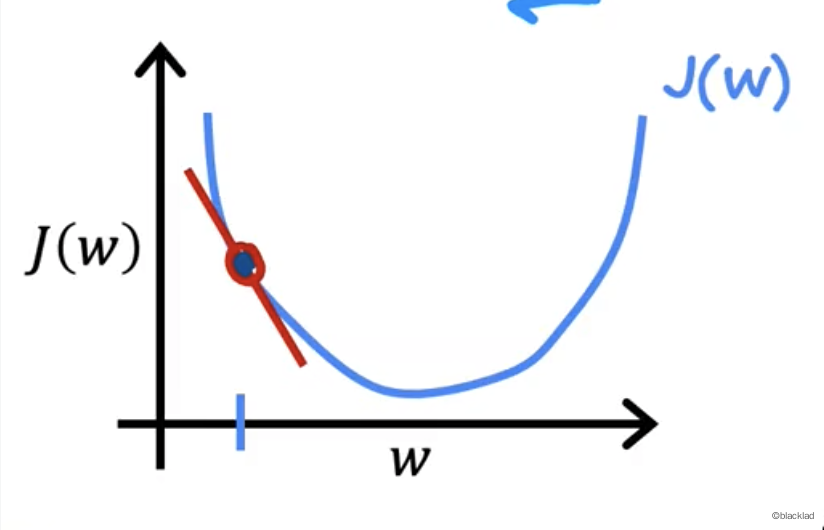
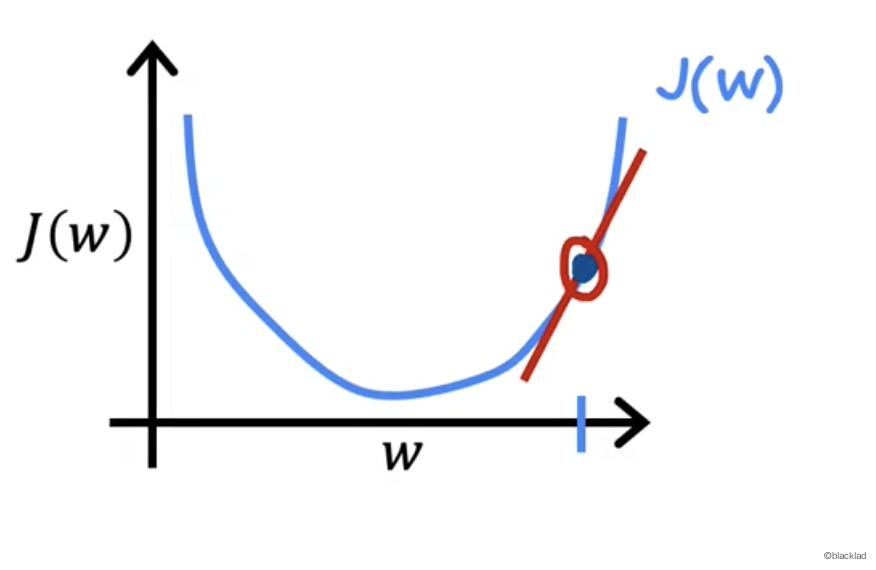
易知这点的导数小于 0 ，α 大于0，所以 w 的值增大。

6 学习率α

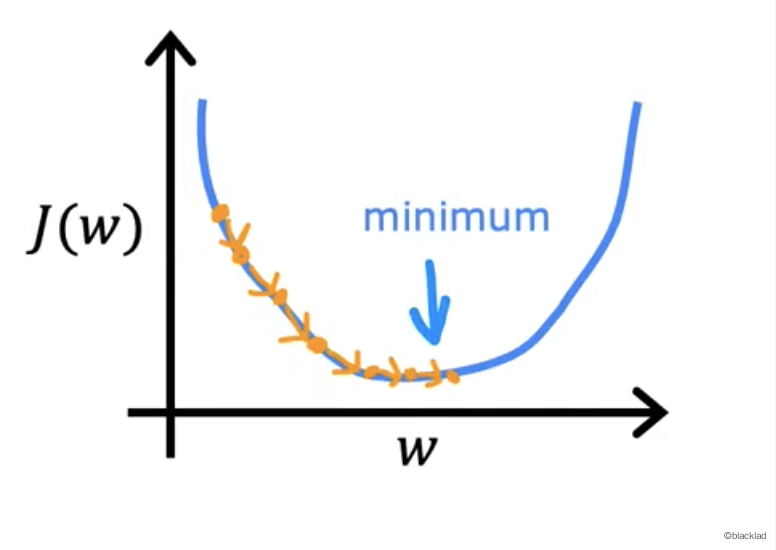
当学习率 α 非常小的时候，比如0.0000001，乘以导数的结果也非常小，会导致 w 每次的步幅非常小，抵达最小值需要非常多步，速度会变慢。

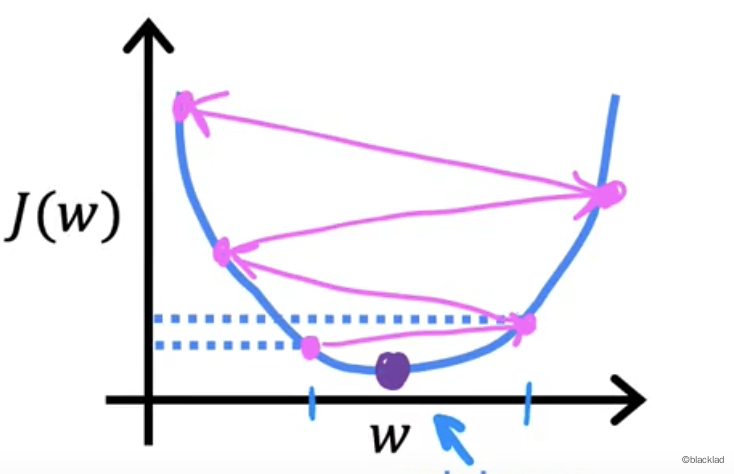
当学习率 α 比较大时，w 的值改变后，超过关于 J 函数局部最小值的对称点时，会离最小点所在的位置越来越远（导数的绝对值在变大，α乘以导数的值也变大），所以算法无法收敛，或者发散。

7 局部极小值

对于一些函数，从起始点开始，可能会有不同的路线得到不同的结果。结果不一定是函数的最小值，只是局部的极小值。

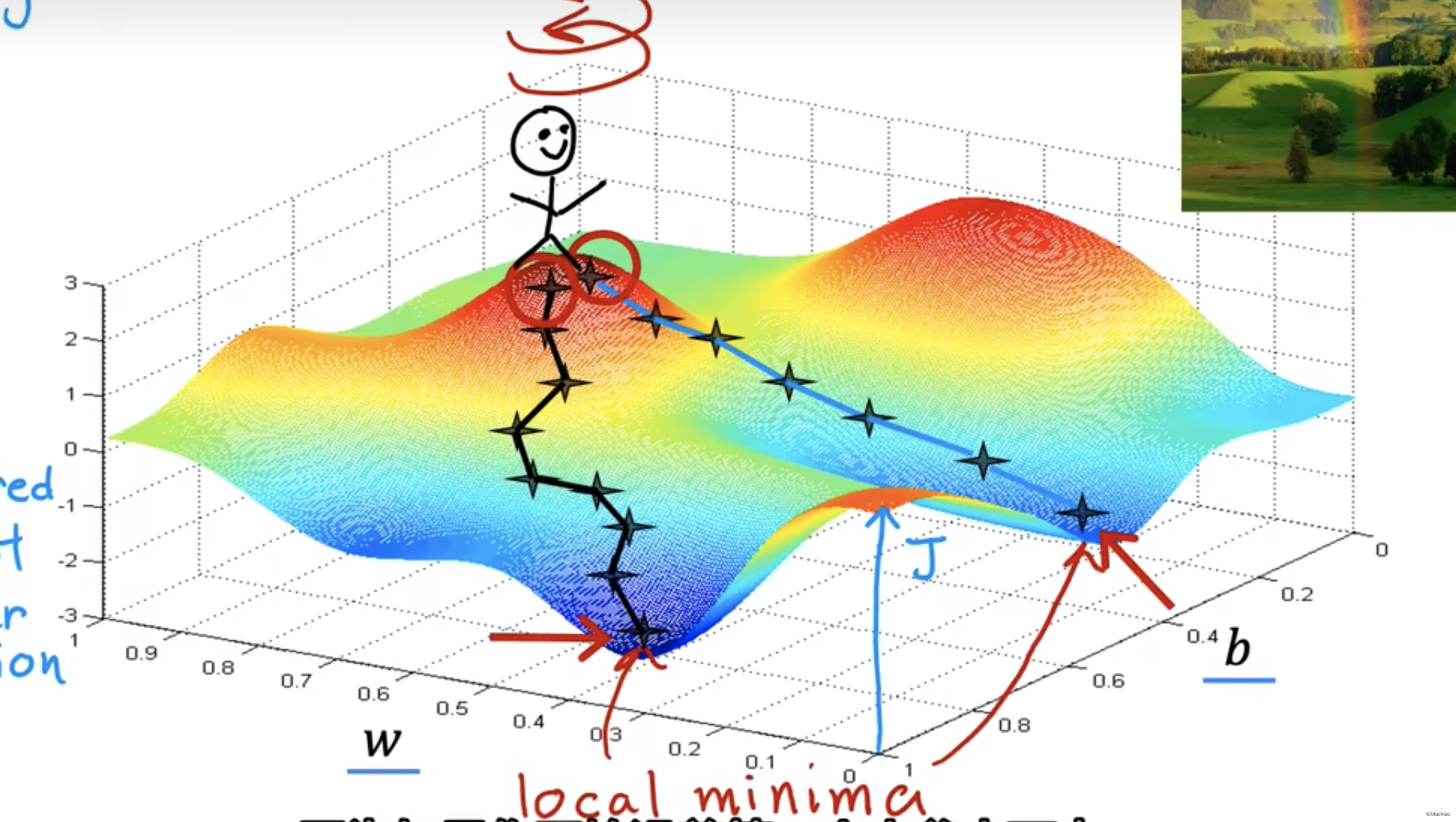
例如当 w 在5时，此时不是函数的最小值，但函数的导数为 0，所以 $α\frac{∂}{∂w}J(w)$ 为0，导致 w 的值就不会改变了，只能达到局部最小值。

对于线性函数，是一个凸函数，形状像碗一样，一定会有最小值。

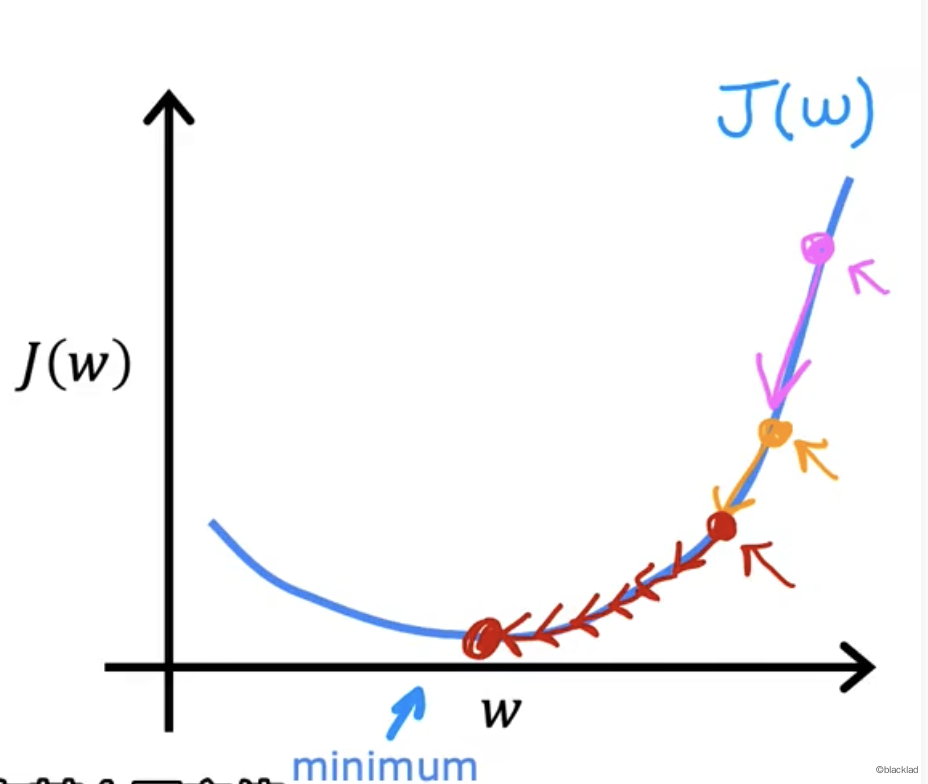
7.1 固定学习率

当学习率固定时，代价函数越接近最小值，导数的值会变小，w 更新的值也会变小

8 线性回归梯度下降

8.1 偏导数的推导

image-20240703224421792

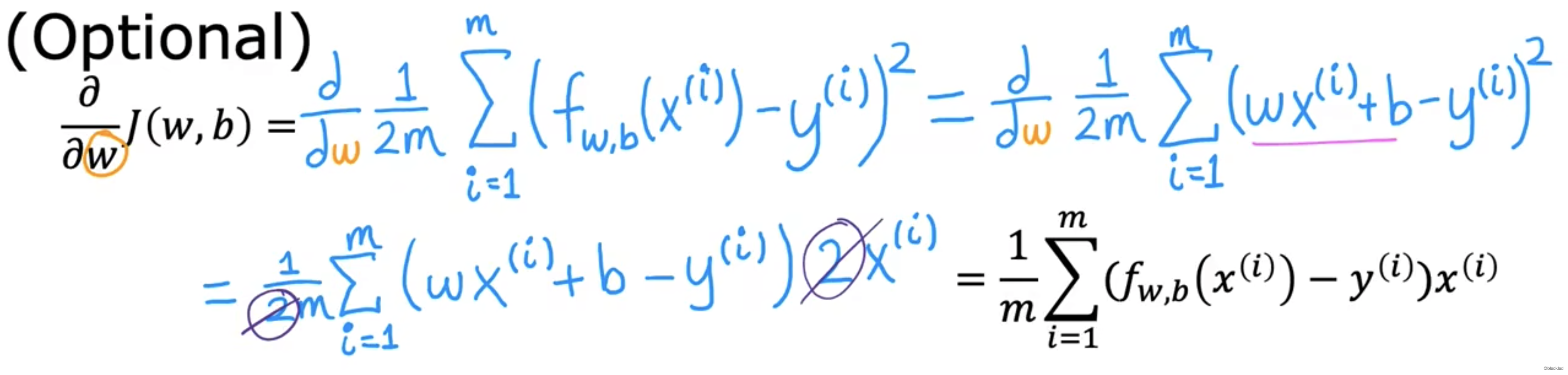
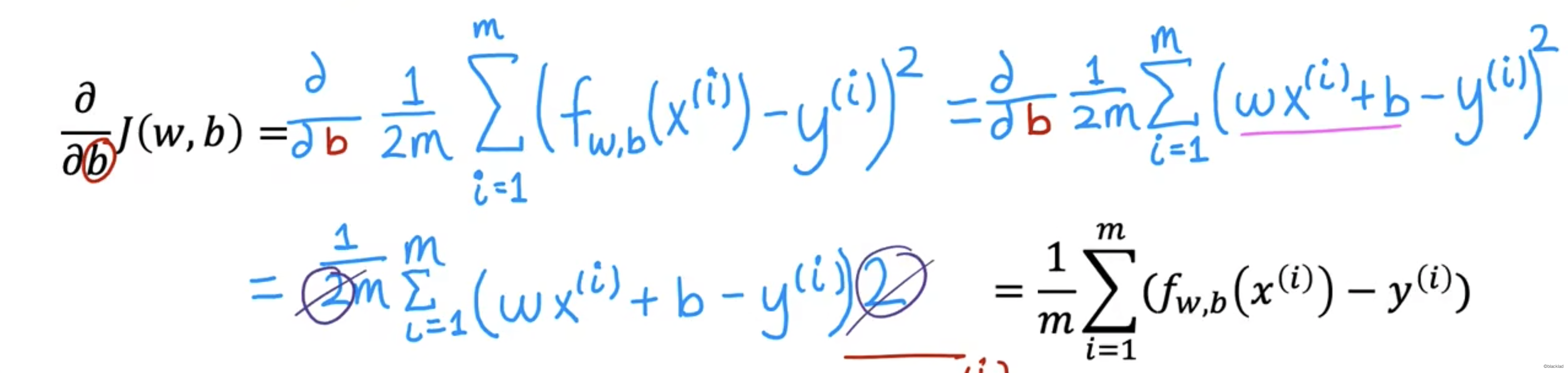
即：

$$w = w - α\frac{1}{m} \sum\limits_{i=1}^m(f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)}$$

$$b = b - α\frac{1}{m} \sum\limits_{i=1}^m(f_{w,b}(x^{(i)}) - y^{(i)})$$

8.2 例子

梯度下降的过程中，J 的在值不断的靠近最小值。

9 批量梯度下降

Batch gradient descent

指在梯度下降的每一步中，都使用所有的训练数据。