因为逻辑回归的输出为概率。所以我们会选择一个阈值,当概率大于这个阈值时,结果就是1。这个阈值就是决策边界。
通常会选择一个阈值 0.5:
对于 fw,b(x)=g(z)=g(wx+b)=1+e−(wx+b)1
fw,b(x)>=0.5 时,预测的结果 y 为 1,此时 z >= 0,即wx+b>=0
fw,b(x)<0.5 时,预测的结果 y 为 0,此时 z < 0,即wx+b<0
当 z=wx+b,决策边界为一条直线。当 z 为其他高阶的多项式时,决策边界为更复杂的曲线。
红叉表示正向示例,蓝圈表示反向示例。有两个输入特征 x1 和 x2
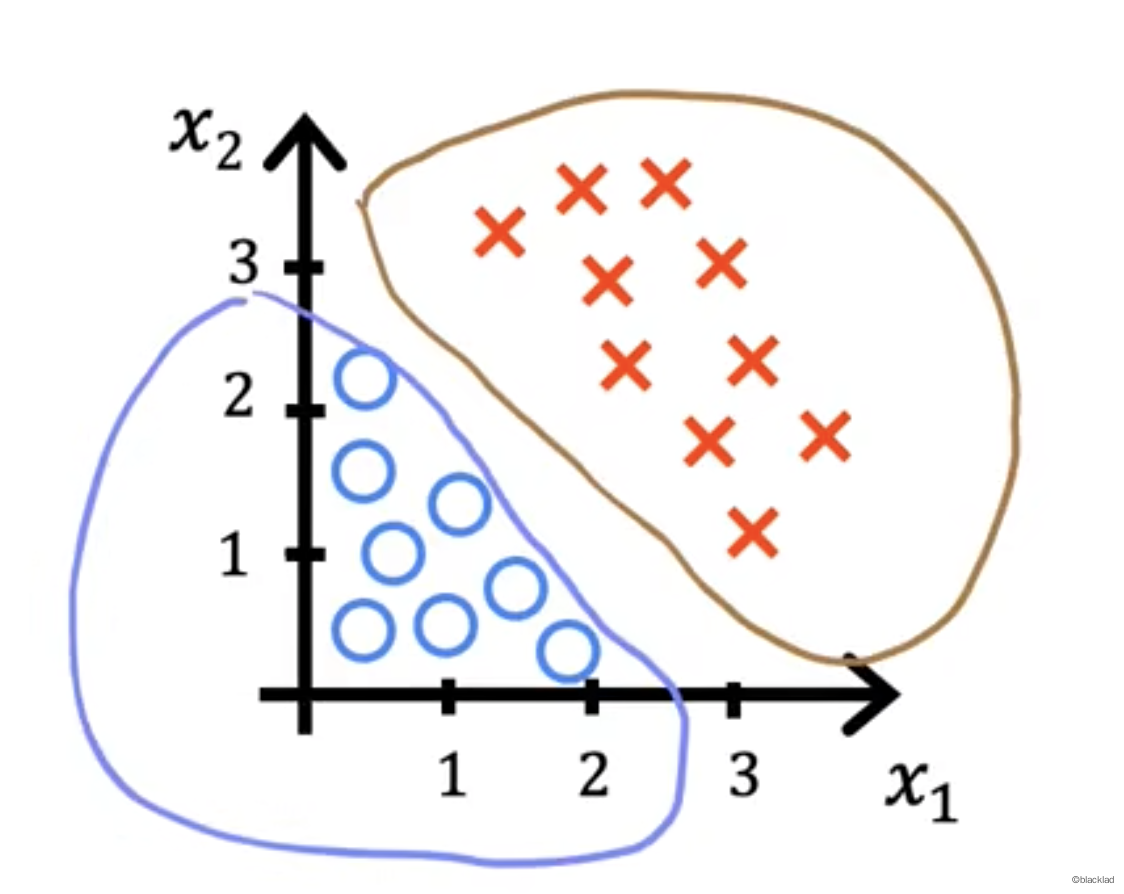
fw,b(x)=g(z)=g(w1x1+w2x2+b)=1+e−(w1x1+w2x2+b)1
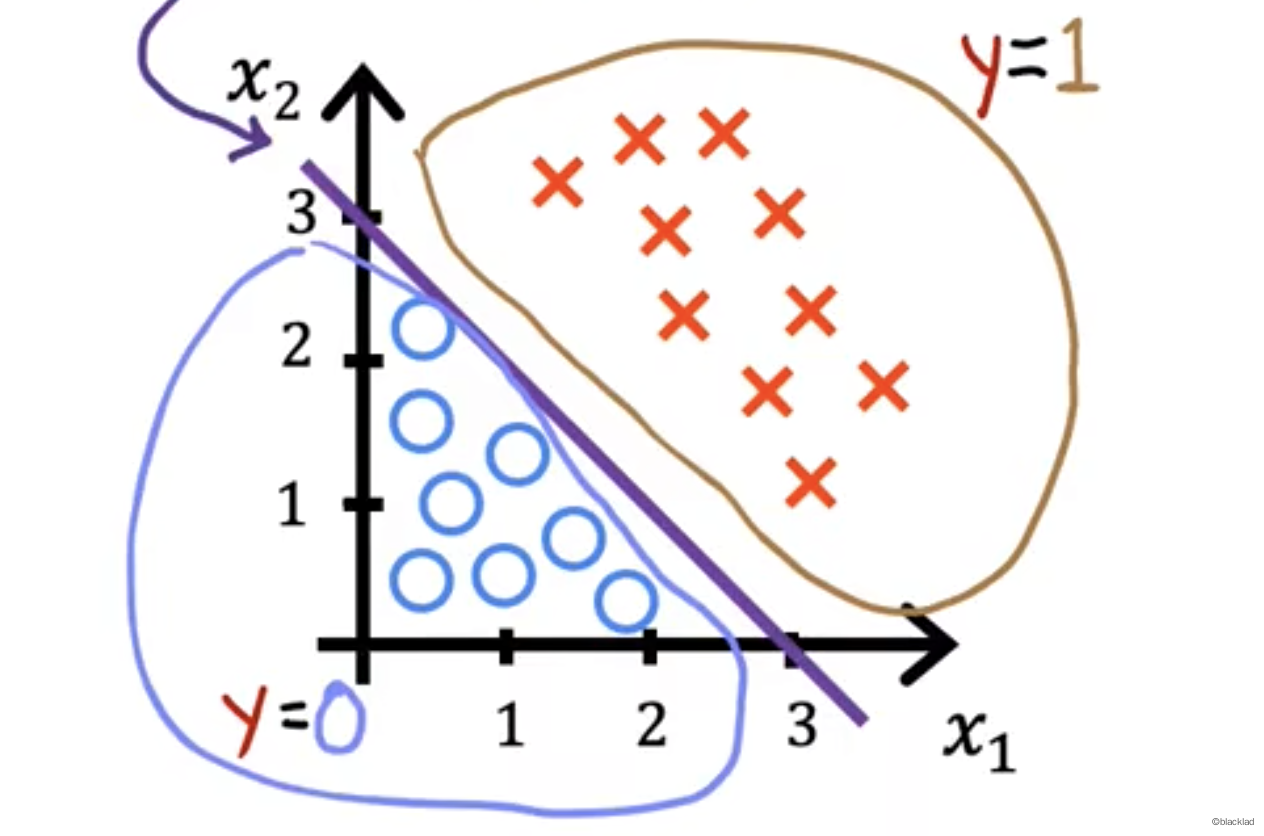
得到的决策边界如下图紫色的线,z=w1x1+w2x2+b=0,紫色的线的左下方的坐标带入可以得到z < 0,紫色的线的右上方的坐标带入可以得到 z >= 0。
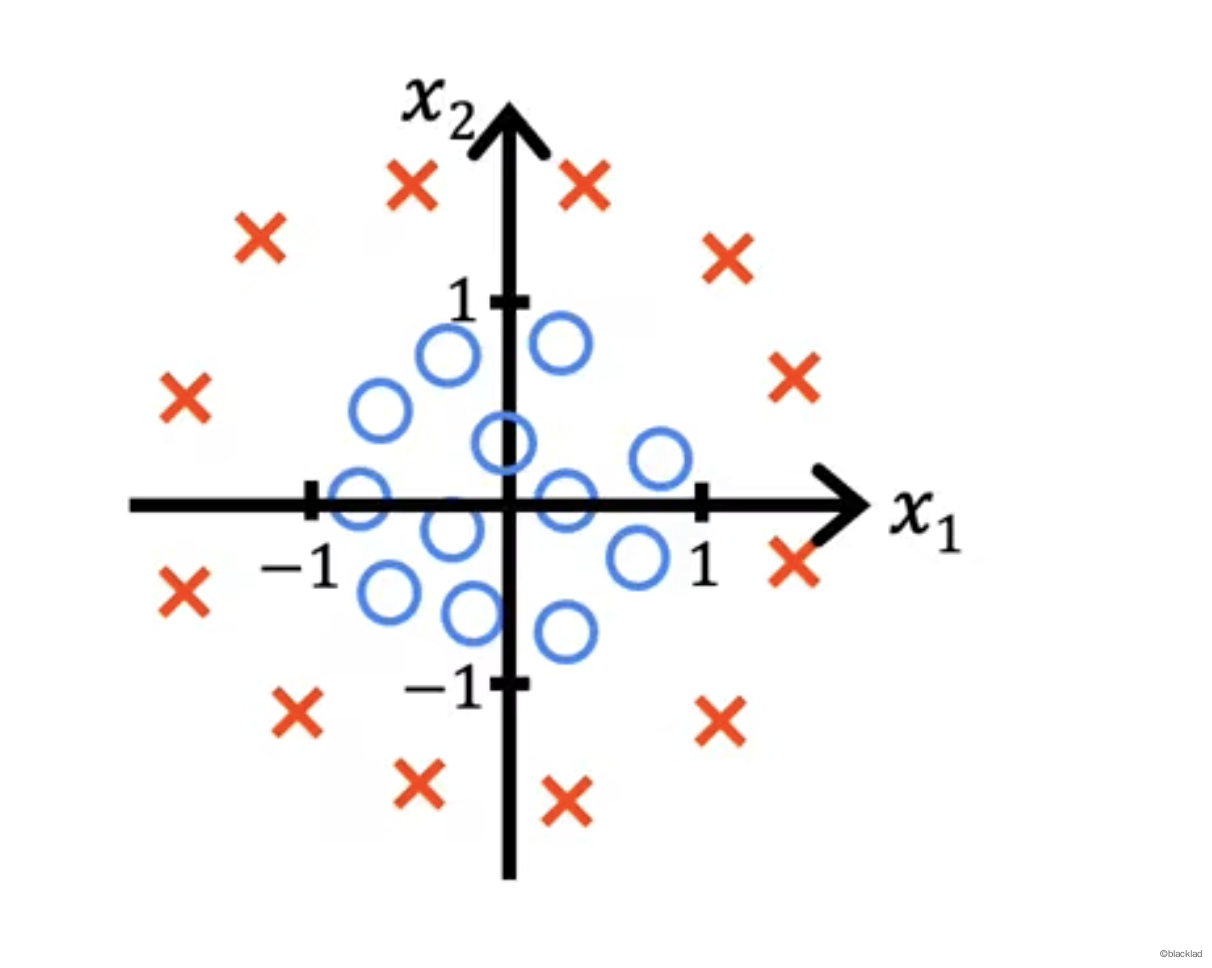
红叉表示正向示例,蓝圈表示反向示例。有两个输入特征 x1 和 x2。但是可以看出线性的无法将区域分成正向和反向两部分。
$$ f_{\vec{w},b}(\vec{x}) = g(z) = g(\vec{w_1}\vec{x_1^2} + \vec{w_2}\vec{x_2^2} + b) = \frac{1}{1+e^{-(\vec{w_1}\vec{x_1^2} + \vec{w_2}\vec{x_2^2} + b)}} $$
得到的决策边界为下图中的圆。z=w1x12+w2x22+b=0,在圆的内部 z 的值小于0,在圆的外部z的值大于0.
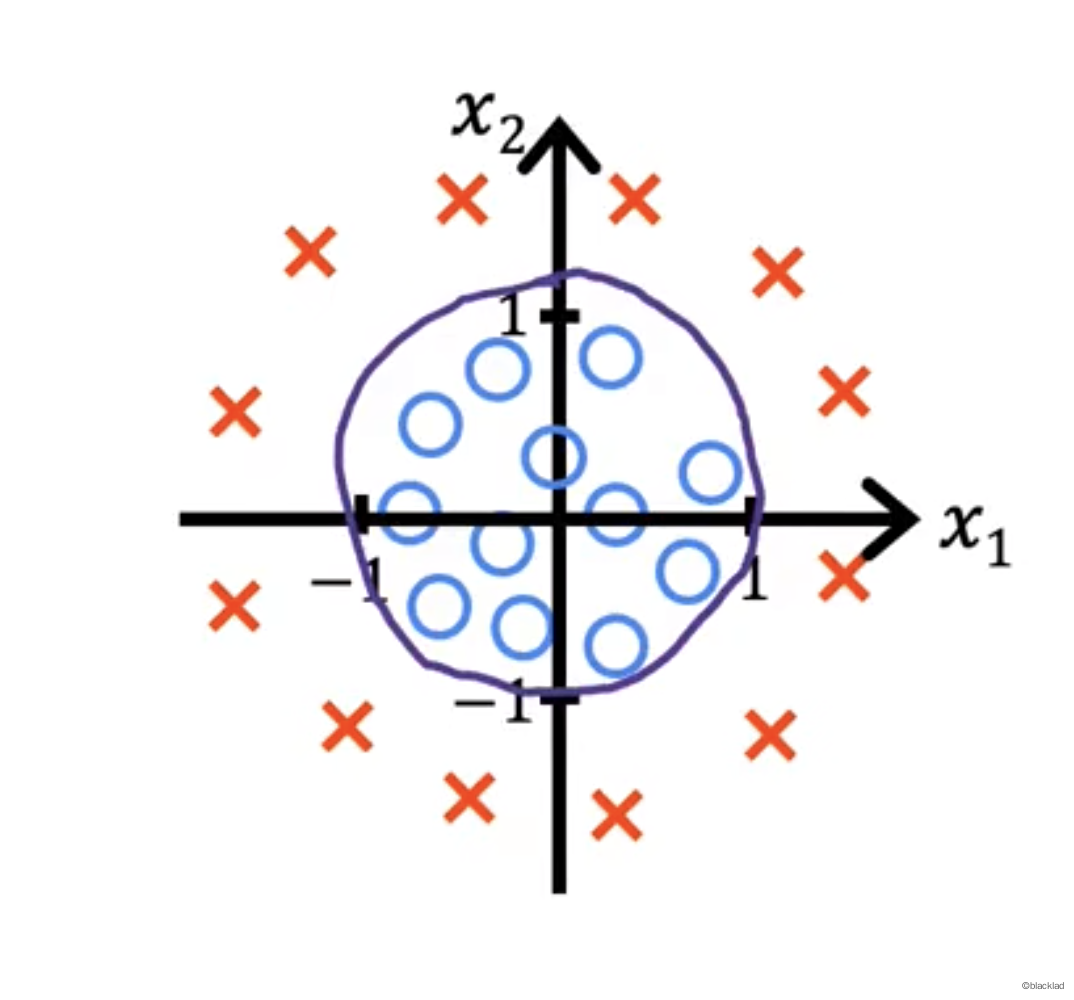
使用更高次的项可以得到各种曲线的决策边界。
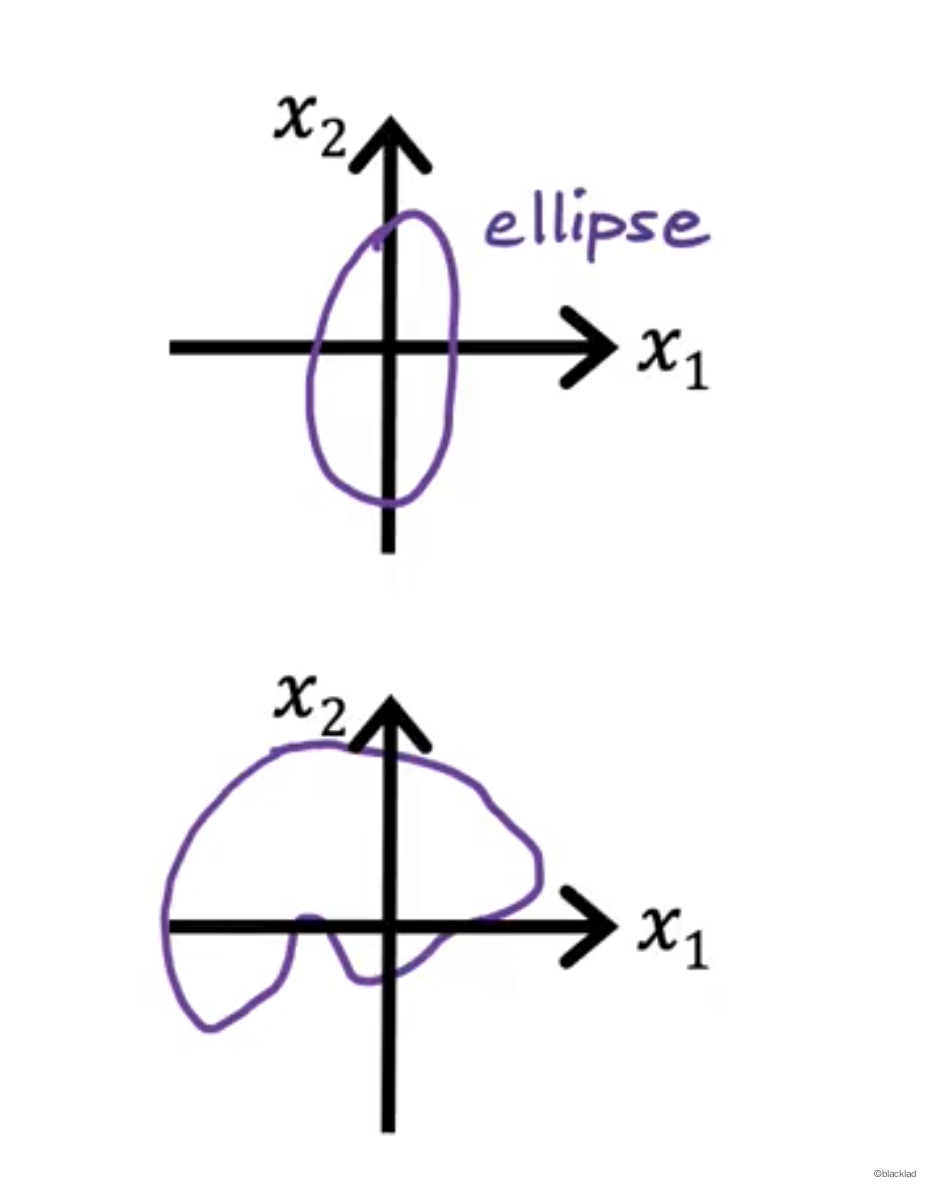


 $$ f_{\vec{w},b}(\vec{x}) = g(z) = g(\vec{w_1}\vec{x_1^2} + \vec{w_2}\vec{x_2^2} + b) = \frac{1}{1+e^{-(\vec{w_1}\vec{x_1^2} + \vec{w_2}\vec{x_2^2} + b)}} $$
$$ f_{\vec{w},b}(\vec{x}) = g(z) = g(\vec{w_1}\vec{x_1^2} + \vec{w_2}\vec{x_2^2} + b) = \frac{1}{1+e^{-(\vec{w_1}\vec{x_1^2} + \vec{w_2}\vec{x_2^2} + b)}} $$ 

