多类分类与 Softmax 函数

1 多类分类问题

对于多类分类（multiclass classfication problem）问题，输出的目标值有多个可能。

如需要识别手写的数字0-9、流水线产品检测不同类型的缺陷等等。

1.1 与二分类的区别

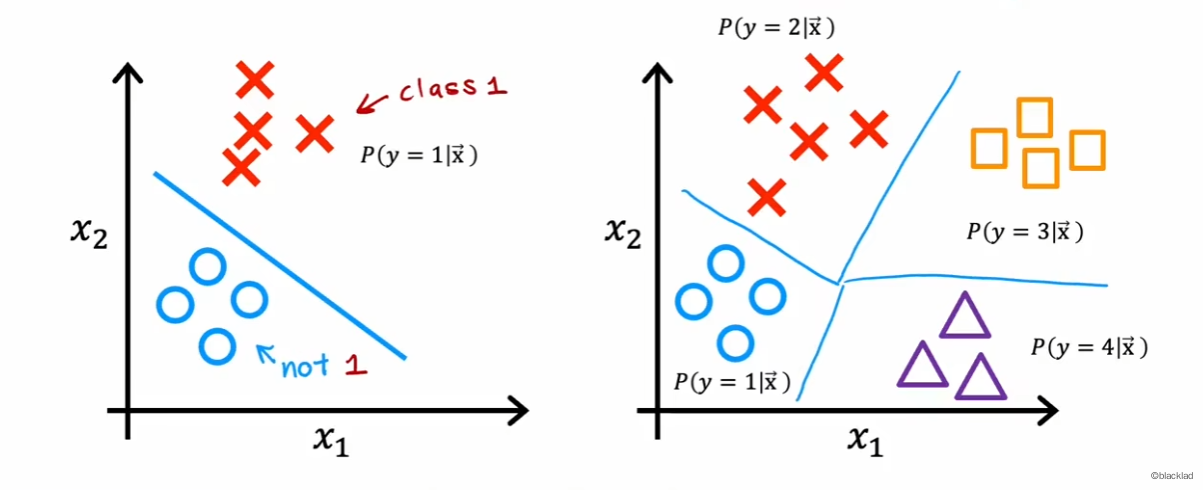
多类分类的结果仍然是有限的多个，不是无穷多个。

算法的目标是找到这样的分界线区分不同的类型。

2 Softmax 函数

假设有一个四种类型的分类任务，z 的定义仍然和 Sigmoid 中的一致，激活函数的概率和为1，同时使用了指数函数，保证最终的概率非负数，且扩大了值得差异。

当只有两种类型时，就会变成逻辑回归（虽然参数不完全一致）。

可以得到 Softmax 的函数如下：

$z_j = \vec{w_j}\vec{x} + b_j j = 1,2,...,N$

$a_{j}=\frac{e^{z_{j}}}{\sum_{k=1}^{N}e^{z_{k}}}$

$a_1 + a_2 + ... + a_N = 1$

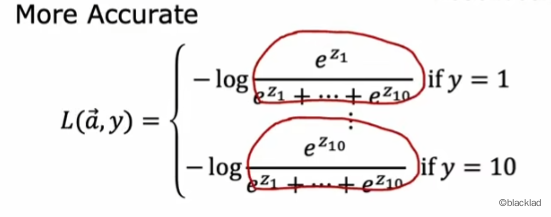
3 Softmax 损失函数

参考下图，逻辑回归的 loss 函数可以转换为：

$$loss(a_1,...,a_N,y)= \begin{cases} -\log a_1 & \mathrm{if}y=1 \\ -\log a_2 & \mathrm{if}y=2 \\ \end{cases}$$

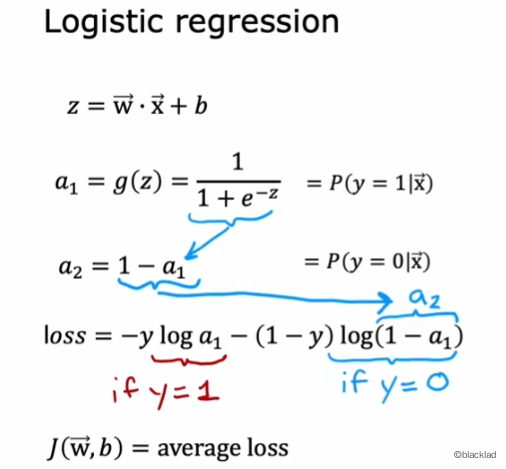
可以得到 Softmax 的 loss 函数（稀疏分类交叉熵 (Sparse Categorical Crossen tropy)）：

$$loss(a_1,...,a_N,y)= \begin{cases} -\log a_1 & \mathrm{if}y=1 \\ -\log a_2 & \mathrm{if}y=2 \\ ... \\ -\log a_N & \mathrm{if}y=N & \end{cases}$$

loss 对数函数取负，当 $a_j$ 越接近 1 时，对应的的损失越接近 0，符合损失函数的定义。

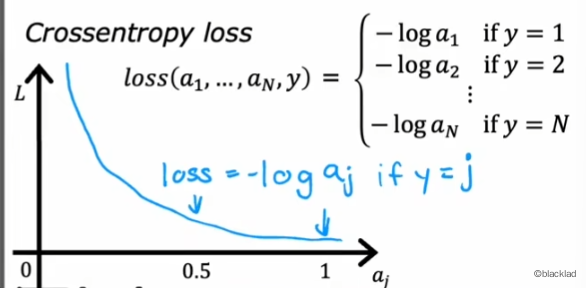
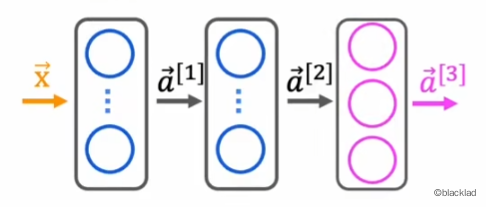
4 神经网络的 Softmax

使用神经网络解决多分类问题时，将输出层更改为 Softmax 函数，有多少个类别，就有多少个输出单元。

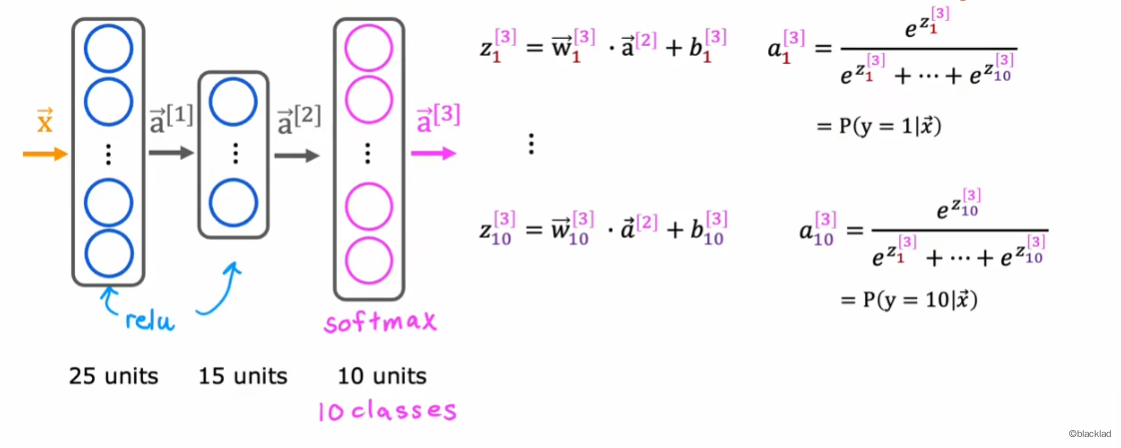
与其他的激活函数不同，Softmax 的 $a_j$ 不止取决于 $z_j$，而是取决于所有的输出 $z_1 z_2 ... z_N$，所以 Softmax 需要同时计算出所有的神经元的输出。

4.1 代码

5 提高数据精度

由于计算机中浮点数的计算会丢失精度（用二进制存储），对浮点数公式

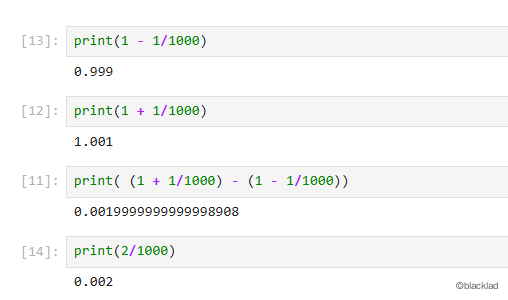
通过简化公式，直接计算最终的结果会减少误差。

对于神经网络的输出层，可以不计算中间的变量 $a_j$，直接将 $z_j$ 代入损失函数中，Tensorflow 会对表达式重排，减少误差。

将神经网络输出层的激活函数换成线性函数，得到 $z_j$，然后修改损失

对于 Tensorflow 在损失函数中可以添加 from_logits=True 的参数。

同时预测的的结果，需要经过softmax函数进行转换得到最终的值。

6 多标签分类

多标签分类是对于单个输入，输出多个不同的标签。比如在一张图中，识别出汽车、公交车、行人等。

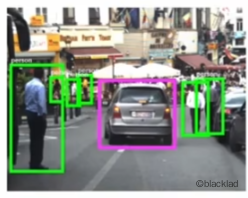
预测的结果是一个向量。

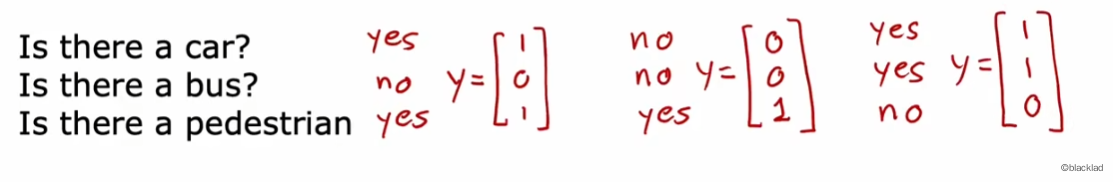
无需使用三个单独的神经网络分别判断，可以定义一个输出层有三个单元的神经网络模型，使用 Sigmoid 函数作为激活函数。